Параметрический резонанс

Незатухающие колебания в колебательной системе с затуханием могут поддерживаться не только внешней периодической силой направленной вдоль траектории движения совершающего колебания тела, но и периодическим изменением параметра колебательной системы. При определенных условиях может быть реализован параметрический резонанс.

Рассмотрим простейший пример, математический маятник, длина нити подвеса которого периодически меняется. При прохождении телом положения равновесия нить укорачивается на величину 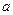, которая много меньше длины маятника (), а в положении, соответствующем максимальному отклонению, удлиняется на величину 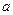. В течение каждого периода изменение длины будет происходить два раза, т.е. частота модуляции параметра колебательной системы в два раза больше собственной частоты колебаний маятника. Мы предполагаем, что изменение длины происходит мгновенно. Это, конечно, не соответствует действительности, однако, такой качественный подход позволяет достаточно просто и наглядно изложить суть изучаемого явления.

При укорачивании нити мы совершаем работу против силы тяжести и против центробежной силы

,

при удлинении нити работу совершает сила тяжести

где 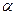- угол максимального отклонения маятника от положения равновесия. Таким образом, за время равное половине периода над системой совершается работа

Как и ранее, определим значение центробежной силы через угол максимального отклонения 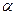. Получим и перепишем уравнение для 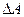в виде:

.

Это работа, совершаемая над маятником за половину периода колебаний, следовательно, за период она составит величину:

()

которая идет на увеличение энергии колебательного движения . Так как , то , где 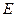полная энергия колебаний, и можно считать, что в среднем за период половина полной энергии колебательного движения тела находится в потенциальной форме, а другая половина – в кинетической, т.е. имеем:

.

Таким образом, уравнение () может быть представлено в виде:

.

Введя обозначение: , получим:

,

уравнение, описывающее в общепринятой форме изменение энергии колебательной системы при параметрическом резонансе:

Видно, что за каждый период колебаний маятник будет увеличивать свою энергию пропорционально величине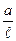и тем больше, чем больше у него была энергия в предыдущий период.

Преобразуем полученное уравнение зависимости энергии колебаний от времени к виду:

и интегрируя его получим: . Предполагая, что в момент времени 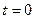полная энергия колебаний составляла величину , определим постоянную интегрирования, , и получим зависимость энергии колебаний от времени в виде:

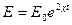
Так как 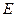~, где 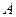- амплитуда колебаний, имеем:

.

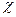называется коэффициентом нарастания колебаний.

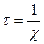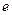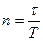Видно, что за время амплитуда колебаний увеличится в раз. называется время нарастания колебаний. За время система совершает колебаний (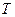-период колебаний). Величина называется логарифмическим инкрементом колебаний.

Для рассматриваемого случая, зависимость смешения тела совершающего колебания от времени имеет вид:

.

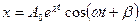Существенно, что при наличии силы вязкого трения, которая пропорциональна скорости движения тела, рост амплитуды колебаний не будет происходить до бесконечности.

Также существенно то, что параметрическая раскачка колебаний может быть реализована только в том случае, если в начальный момент времени существуют, пусть даже бесконечно малые, но отличные от нуля, колебания, существует .

3.7. Сложение колебаний одинакового направления

Этот случай часто реализуется в практической деятельности человека: вибро-машины, виброгасители, рессоры и т.д.

Рассмотрим тело, участвующее в двух однонаправленных колебаниях одновременно. Примером устройства, реализующего эту ситуацию, может быть пружинный маятник, точка подвеса которого подвешена к неподвижной опоре на пружине.

Пусть соответствует колебаниям тела относительно точки подвеса, а - колебаниям точки подвеса относительно неподвижной опоры. Суммарное смешение, очевидно, будет равно:

.

Рассмотрим два случая:

1. Пусть . Тогда

,

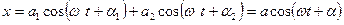где ,

.

Видим, что амплитуда результирующих колебаний зависит от разности начальных фаз.

Если , то:

,

и в случае , амплитуда колебаний увеличивается и становится равной .

Если , то амплитуда результирующих колебаний становится равной нулю.

Итак, в зависимости от начальной разности фаз, колебания либо усиливаются, либо взаимно гасятся.

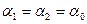2. Пусть , а . Тогда:

,

где

.

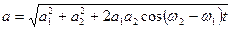Видим, что амплитуда колебаний зависит от времени, следовательно, эти колебания уже не являются гармоническими.

Если , то:

.

Итак, сложение однонаправленных колебаний разной частоты приводит к возникновению колебаний, амплитуда которых пульсирует во времени. Эти пульсации называются биениями.

Дата добавления: 2014-01-05