
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Третя форма суперпозиційного інтегралу Дюамеля
|
|
|
|
Розглянемо електричне коло з нульовими початковими умовами, на вхід якого подається сигнал напруги довільної форми u(t).
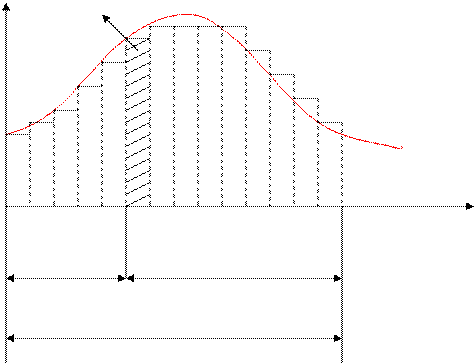 u(t)
u(t) 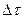
0 t
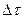 2
2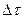 … n
… n
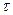
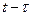
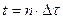
Визначимо закон зміни перехідного струму 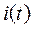 , якщо імпульсна характеристика кола дорівнює
, якщо імпульсна характеристика кола дорівнює 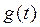 .
.
Замінимо 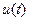 прямокутними імпульсами з амплітудою
прямокутними імпульсами з амплітудою 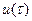 та тривалістю
та тривалістю 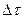 .
.
Кожний імпульс напруги інтенсивністю 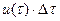 , який діє на електричне коло в момент часу
, який діє на електричне коло в момент часу 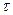 , створює складову перехідного струму, яка в момент часу t буде дорівнювати
, створює складову перехідного струму, яка в момент часу t буде дорівнювати
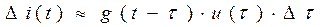 ,
,
де 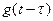 – імпульсна характеристика (провідність) для імпульсної функції, що запізнюється на час
– імпульсна характеристика (провідність) для імпульсної функції, що запізнюється на час 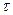 .
.
Повний перехідний струм буде дорівнювати сумі складових перехідного струму, який обумовлений кожним імпульсом напруги і для моменту часу 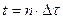 буде приблизно дорівнювати:
буде приблизно дорівнювати:
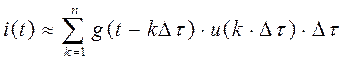 .
.
Якщо перейти до ліміту при 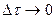 , то отримаємо точне рівняння для перехідного струму:
, то отримаємо точне рівняння для перехідного струму:

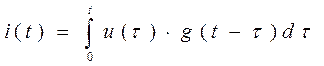 .
.
Це рівняння називається третьою формою суперпозиційного інтегралу Дюамеля.
Замінимо 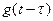 на
на 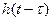 .
.
В загальному випадку

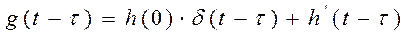 ,
,
тоді

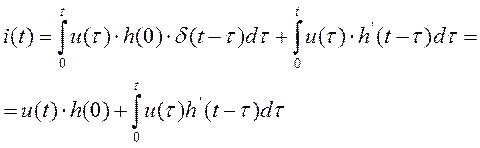
Це рівняння називається розгорнутою третьою формою інтегралу Дюамеля при 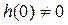 .
.
Для даного випадку 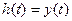 , тоді отримаємо
, тоді отримаємо

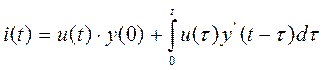 .
.
Порядок застосування третьої форми інтегралу Дюамеля такий же, як і для першої форми. Для порівняння наводимо рівняння для перехідних струмів, що отримані при використанні третьої форми інтегралу Дюамеля, для того ж закону напруги, який раніше використовувався для першої форми інтегралу Дюамеля
1. при 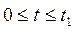 ,
, 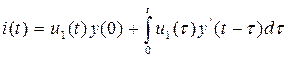 ,
,
2. при 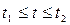 ,
, 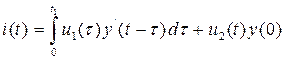 ,
,
3. при 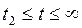 ,
, 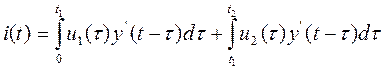 .
.
Ці рівняння простіші попередніх тому, що не мають доданків, які враховують складові перехідного струму, що обумовлені стрибками напруг.
Крім першої та третьої форм інтегралу Дюамеля для розрахунку перехідних процесів застосовуються друга та четверта форми. При цьому другу форму отримуємо з першої, а четверту – із третьої шляхом заміни в їх підінтегральних виразах 
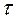 на
на 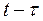 , а
, а 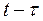 на
на 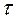 . Тоді друга та четверта форми інтегралу Дюамеля будуть мати вигляд:
. Тоді друга та четверта форми інтегралу Дюамеля будуть мати вигляд:
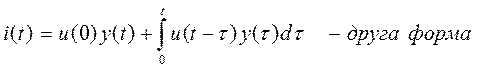 ,
,
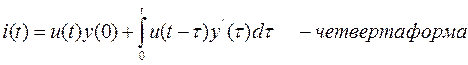 .
.
Така заміна часу рівнозначна тому, що результуюча дія ступінчастих або імпульсних сигналів, якими приблизно замінений вхідний сигнал, здійснюється, починаючи з моменту часу 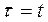 та закінчуючи часом
та закінчуючи часом 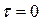 , тобто із кінця до початку.
, тобто із кінця до початку.
Застосування цих або інших форм інтегралу Дюамеля залежить від конкретного випадку. При 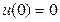 краще застосовувати першу або другу форми, а при
краще застосовувати першу або другу форми, а при 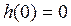 - третю або четверту форми тому, що в цьому випадку перші доданки обертаються в нуль.
- третю або четверту форми тому, що в цьому випадку перші доданки обертаються в нуль.
Третю форму інтегралу Дюамеля краще застосовувати тоді, коли вхідна напруга має розриви неперервності першого роду тому, що в цьому випадку немає складових, які обумовлені стрибками напруги.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 421; Нарушение авторских прав?; Мы поможем в написании вашей работы!