Спектр последовательности прямоугольных импульсов

Периодический процесс в виде последовательности импульсов, аналитически может быть представлен

U₀ -(nT+t)≤t≤(nT+t)

u(t)=í (4)

0 -(nT+t)>t>(nT+t)

для не симметричного расположения импульса относительно точки отсчета и в виде

U₀ -(nT+t/2)≤t≤(nT+t/2)

u(t)=í (5)

0 -(nT+t/2) >t>(nT+t/2)

для симметричного расположения. Длительность импульса t определяется как разность отсчетов между двумя моментами времени t =t₂-t₁.

Подставляя значения для u(t) в (2) найдем коэффициенты ряда a₀, a_k, b_k в виде

, которое определяет среднее значение функции,

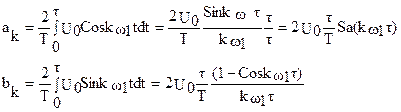, (6)

так как , то, подставляя найденные коэффициенты, получим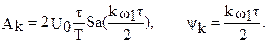

Отношение t/T называют скважностью.

Используя полученные формулы, периодический сигнал может быть представлен в форме

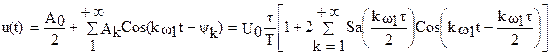если же начало отсчета выбрать в начале координат, то коэффициенты b_k=0 и

формула принимает вид

(7)

Из (7) видно, что спектр последовательности прямоугольных импульсов состоит из бесконечного числа гармонических составляющих с частотами кратными частоте w₁, амплитуда которых изменяется в соответствии с функцией Sa(х) и, тем, самым определяет форму спектра

A(w)=A_k=2U₀(t/T)Sa(kw₁t)=2U₀(t/T)Sa(wt) (8)

в виде огибающей амплитуд, принимающей на частотах (2nπ/t)=w₀ нулевые значения, а на частотах [(2n+1)π/t]=w_m максимальные. На частоте w₀=0, значение огибающей равно (2U₀t/T).

Рис.1. Последовательность прямоугольных импульсов и ее спектр

Сигналы типа меандра могут быть представлены в виде

u(t)=(4U₀/π)[(Sinw₁t)+1/3(Sin3w₁t)+1/5(Sin5w₁t)+...], а если сигнал имеет симметричное расположение относительно точки отсчета, то в виде

u(t)=(4U₀/π)[Cosw₁t-1/3(Cos3w₁)+1/5(Cos5w₁t)-...].

Дата добавления: 2014-01-05