Спектр непериодических сигналов

Спектр прямоугольного импульса

Модуль спектра прямоугольного импульса протяженностью Δх с амплитудой U₀ имеет вид:

U₀ |x| ≤ Δx/2

U(x) = {

0 |x| > Δx/2

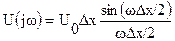
Рис.2. Прямоугольный импульс и его спектр

Предположим, что сигнал задан в виде функции времени, удовлетворяющей условию Дирихле и абсолютной интегрируемости, то есть при t ®µ u(t) ®0, а 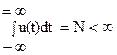, действующей в пределах интервала t₁<t<t₂.

Превратим u(t) в периодическую функцию u₁(t) с произвольным периодом T>(t₂-t₁) и, применив к ней разложение в ряд Фурье, запишем

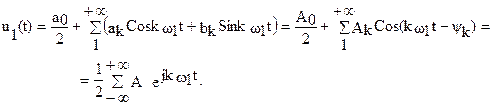(9) из принятых условий следует, что при T®µ u₁(t) ® u(t), а число гармонических составляющих растет, так как f₁=(1/T)=(w₁/2π) ® 0, и, следовательно, расстояние между гармониками стремится к df, а спектр в силу этого становится сплошным и u₁(t) можно переписать в виде

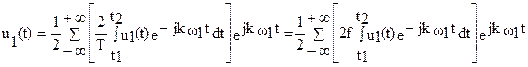а так как при T®µ 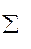переходит в 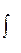, f₁ в df, а kw₁ в w, то

окончательно полученное соотношение представим в виде

(10)

Эти соотношения называют обратным и прямым преобразованием Фурье, соответственно. Физически они означают, что если известно спектральное распределение энергии сигнала, то временная форма сигнала может быть получена, если воспользоваться обратным преобразованием Фурье. Если же задана временная форма сигнала, то распределение его энергии по спектру определяется формулой прямого преобразования. Обычно называют спектральной плотностью или комплексным спектром Фурье сигнала u(t). Так как df = dw, то=2π.

Для комплексного спектра, также как и для любой комплексной величины справедливы соотношения

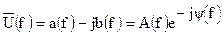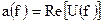, где , а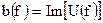

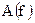- называют спектром амплитуд, а 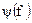- называют спектром фаз.

Дата добавления: 2014-01-05