Поле точечного заряда q

Примеры применения теоремы Гаусса.

Теорему Гаусса удобно применять для определения напряжённости поля в случаях, когда картина силовых линий обладает какой-либо симметрией.

Пусть q >0. Возьмём в качестве поверхности S сферу радиусом R с центром в месте нахождения заряда. На поверхности этой сферы вектор 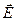сонаправлен с вектором нормали 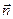к поверхности сферы, поэтому 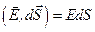. В каждой точке поверхности сферы

.

.

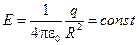Так как площадь поверхности сферы 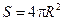, то поток вектора напряженности

.

2) Поле бесконечной прямой заряженной нити. Пусть нить заряжена с линейной плотностью заряда l>0.

Как мы уже знаем, силовые линии поля направлены перпендикулярно нити и картина поля в целом обладает осевой симметрией относительно нити.

Найдем поток вектора напряжённости через поверхность прямого цилиндра радиуса R и высоты L, ось которого совпадает с осью цилиндра.

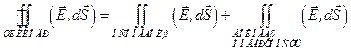
На основаниях цилиндра векторы 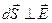, поэтому .

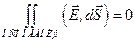На боковой поверхности 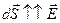, поэтому .

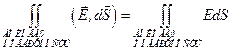Т.к. картина поля осесимметрична, то величина Е зависит только от расстояния до нити, поэтому на боковой поверхности этого цилиндра величина E =const.

.

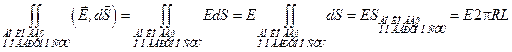По теореме Гаусса . Но внутри цилиндра находится часть нити длиной L, поэтому 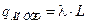. Тогда 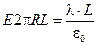и для величины Е получаем: .

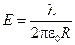3) Поле бесконечной заряженной плоскости. Пусть поверхностная плотность заряда s>0. Картина силовых линий симметрична относительно плоскости. Найдём поток через поверхность прямого цилиндра, основания которого параллельны плоскости, и расположенного так, что плоскость делит цилиндр пополам.

.

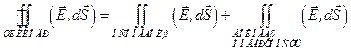Тогда .

На основаниях величина Е будет одинаковой: .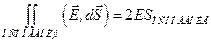

Величина заряда внутри цилиндра .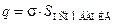

Поэтому по теореме Гаусса имеем: 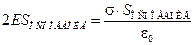, откуда .

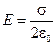4) Поле тонкостенной (полой) заряженной сферы.

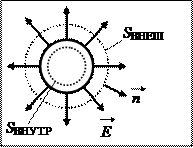Картина силовых линий обладает центральной симметрией относительно центра сферы, поэтому величина напряженности поля зависит только от расстояния до центра сферы.

Сначала в качестве поверхности рассмотрим концентрическую сферическую поверхность, находящуюся внутри сферы:

.

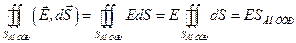Но внутри сферы зарядов нет, поэтому 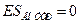. Таким образом, напряжённость поля внутри сферы равна нулю: .

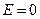Теперь в качестве поверхности рассмотрим концентрическую сферическую поверхность радиуса R, охватывающую сферу. Тогда

.

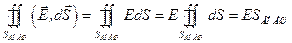Эта поверхность охватывает сферу целиком, поэтому 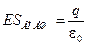, откуда

.

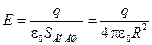5 ) Поле, создаваемое полым бесконечным заряженным цилиндром радиуса R.

Картина силовых линий симметрична относительно оси цилиндра.

Внутри цилиндра Е =0, а снаружи 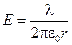, где l - линейная плотность заряда цилиндра, r - расстояние от оси цилиндра. Если для цилиндра задана поверхностная плотность заряда s, то, т.к. заряд куска цилиндра длиной L равен 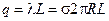, откуда получаем 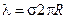, поэтому

.

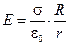6) Поле, создаваемое шаром радиуса R и заряженным равномерно зарядом q. Картина силовых линий обладает центральной симметрией. Выделим внутри шара сферу радиуса r с центром, совпадающим с центром шара. Тогда

.

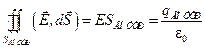Заряд внутри сферы 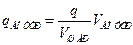, где объём шара 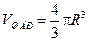, объём внутри сферы

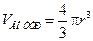, площадь поверхности внутренней сферы 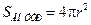. Тогда

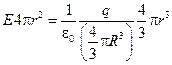, поэтому внутри шара .

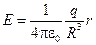Замечание. Это равенство можно записать в векторном виде , где 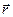- радиус-вектор из центра шара.

Снаружи шара картина поля аналогична уже разобранному полю заряженной сферы

.

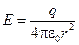На поверхности шара величина напряжённости – непрерывная.

Дата добавления: 2014-01-05