Ширина спектральных линий

Ширина спектральной линии dw - мера немонохроматичности спектральной линии. Её определяют как расстояние между точками контура спектральной линии, в которых интенсивность равна половине её максимального значения. В научной литературе вместо термина «Ширина спектральной линии» иногда используют английскую аббревиатуру FWHM - Full Width at Half Maximum (Полная ширина на половине максимума).

Из возбуждённого состояния атом может перейти спонтанно (самопроизвольно) в более низкое энергетическое состояние. Время, за которое число атомов, находящихся в данном возбуждённом состоянии, уменьшается в е раз, называется временем жизни t возбуждённого состояния. Время жизни возбуждённых состояний атомов имеет порядок 10^-8 – 10^-9 сек. Время жизни метастабильных состояний может достигать десятых долей секунды.

Возможность спонтанных переходов указывает на то, что возбуждённые состояния нельзя рассматривать как строго стационарные. В соответствии с этим значение энергии возбуждённого состояния не является точно определённой величиной и возбуждённый энергетический уровень имеет конечную ширину, поэтому кванты излучения:

h ν = E ₂ - E ₁

не строго монохроматичны, а соответствующая частота перехода с одного энергетического уровня на другой имеет разброс около некоторого значения. Величину этого разброса и характеризуют: «ширина спектральной линии».

Из соотношений неопределённости для времени и энергии: следует, что ширина уровня обратно пропорциональна времени жизни t возбуждённого состояния. Естественную ширину возбуждённого уровня энергии G определяют аналогично - как полную ширину разброса энергии на половине максимума интенсивности излучения, соответствующую переходу с данного уровня энергии. В этом случае: .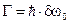

Принято считать, что среднее время жизни возбуждённого состояния t и естественная ширина уровня энергии G связаны соотношением: . Тогда получаем выражение для связи естественной ширины спектральной линии и среднего времени жизни данного возбуждённого состояния: 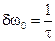. Принимая, что с, находим: 1/с.

Кроме естественной ширины спектральной линии немонохроматичность излучения может быть вызвана и другими причинами. Например, тепловым движением атомов. В этом случае наблюдается доплеровское уширение спектральных линий. Также в процессах испускания фотона атомы приобретают дополнительный импульс «отдачи», что тоже смещает спектральную линию.

Гиромагнитное отношение.

Гиромагнитным отношением называется отношение магнитного момента 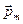к механическому моменту импульса . При классическом рассмотрении движения электрона по орбите это отношение равно: Г= (e – элементарный заряд, m_e – масса электрона.) Знак минус показывает, что векторы 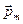и направлены противоположно. Из этого соотношения следует, что величина магнитного момента, связанного с орбитальным движением электрона равна

, а проекция магнитного момента электрона на какое-то направление определяется магнитным квантовым числом m: .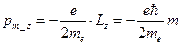

Магнетоном Бора называется величина Дж/Тл.

С учётом этого определения получаем: , .

Спин электрона.

В 1925 г. С. Гаудсмит и Дж. Уленбек выдвинули смелую гипотезу о том, что сам электрон является носителем «собственных» механического и магнитного моментов, не связанных с движением электрона в пространстве. Эта гипотеза получила название гипотезы о спине электрона (от англ. spin – кружение, верчение).

Сначала предполагалось, что спин обусловлен вращением электрона вокруг своей оси. Но такая модель вращающегося заряженного шарика оказалась несостоятельной. Прежде всего, расчёт показал, что ни при каких допустимых скоростях (т. е. меньше скорости света) нельзя вращением электрона индуцировать магнитный момент, равный по величине магнетону Бора. Кроме того, значение гиромагнитного отношения собственного магнитного и механического моментов, рассчитанное для модели вращающегося электрона, оказалось в 2 раза меньше, чем получаемое в опытах.

Модель электрона, вращающегося вокруг своей оси подобно тому, как вращается Земля, двигаясь по околосолнечной орбите, сегодня может использоваться только при популярном изложении свойств атома. Однако термин «спин» сохранился и является общепринятым в современной квантовой физике.

Спин электрона не имеет классического аналога. Он характеризует внутреннее свойство квантовой частицы, связанное с наличием у неё дополнительной степени свободы. Количественная характеристика этой степени свободы – спин 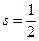- является для электрона такой же величиной, как, например, его масса 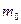и заряд -e.

Для согласования теории и эксперимента Гаудсмит и Уленбек предположили, что по аналогии с орбитальными моментами значения собственных механического и магнитного моментов электрона определяются по следующим формулам:

,

.

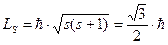Для таких моментов гиромагнитное отношение оказывается в два раза больше гиромагнитного отношения для орбитального движения.

Проекции собственных моментов на выделенное направление z в такой теории определяются спиновым квантовым числом . При этом

,

.

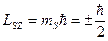Итак мы видим, что значение спинового момента электрона постоянно, а с дополнительной степенью свободы электрона связана z–проекция этого момента, которая определяется спиновым квантовым числом 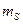и принимает два значения: . О таких двух квантовых состояниях обычно говорят как о состояниях со спином, направленным вверх: 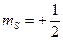или вниз: 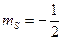. Поэтому, определяя квантовое состояние электрона в любой системе, следует указывать также и ориентацию спина. Набор четырёх квантовых чисел, определяющих квантовое состояние электрона в атоме, представлен ниже в таблице.

Квантовое число	Символ	Возможные значения
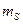
Главное   Орбитальное   Магнитное   Спиновое	n   l   m	1, 2, 3,…   0, 1, 2, 3, … (n – 1)

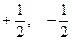
Дата добавления: 2014-01-05