Модель АЧТ

Абсолютно чёрное тело является идеализацией. В природе АЧТ не существует. Однако достаточной хорошей моделью является почти замкнутая колба с двойными стенками (между которыми находится вакуум). В этой колбе имеется малое отверстие. Излучение, вошедшее в отверстие, испытывает многократное отражение от стенок полости и, в конце концов, практически полностью ими поглощается. Т.к. площадь отверстия мала, то вероятность того, что падающее излучение после многократного отражения выйдет из полости, практически равна нулю. Температура стенок полости поддерживается постоянной. Поэтому внутренние стенки полости находятся в термодинамическом равновесии со своим тепловым излучением. Часть этого излучения выйдет через отверстие, и его можно зарегистрировать. Моделью АЧТ является именно отверстие, т.к. из него выходит излучение, близкое к излучению АЧТ.

Экспериментальные данные свидетельствуют о том, спектральная плотность энергетической светимости как функция частоты (или длины волны) имеет глобальный максимум. Соответствующая этому максимуму длина волны уменьшается с ростом температуры АЧТ, или, как принято говорить, смещается в сторону коротких длин волн.

На основе экспериментального исследования теплового излучения Йозеф Стефан (1879г.) и Людвиг Больцман (1884г.) получили зависимость энергетической светимости АЧТ от температуры. По определению, интегральная испускательная способность (энергетическая светимость) равна площади под графиком спектральной плотности энергетической светимости .

Закон Стефана-Больцмана:

гласит, что энергетическая светимость АЧТ прямо пропорциональна 4й степени его абсолютной температуры. (Этот закон следует из законов термодинамики.) Коэффициент пропорциональности носит название постоянной Стефана-Больцмана и численно равен

.

Вильгельм Вин рассмотрел модель АЧТ, в которой одна из стенок полости могла двигаться с некоторой скоростью. Тогда из условия термодинамического равновесия излучения с веществом, учитывая эффект Доплера, он показал, что общий вид спектральной плотности энергетической светимости АЧТ как функции частоты и температуры следующий:

,

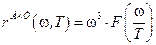где - некоторая функция от отношения . Соответственно, , откуда

.

При этом функция должна иметь максимум, соответствующий определённой длине волны 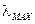. Условие максимума функции приводит к соотношению:

,

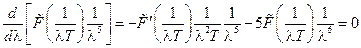откуда после сокращения 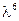и обозначения получим уравнение с одной переменной

.

Т.к. максимум функции существует, то у этого уравнения есть хоть одно решение, соответствующее глобальному максимуму . Тогда . Т.е. длина волны, соответствующая максимуму спектральной плотности энергетической светимости, обратно пропорциональна температуре АЧТ.

Закон смещения Вина.

Длина волны, соответствующая максимуму спектральной плотности энергетической светимости АЧТ обратно пропорциональная температуре АЧТ: .

Константа м×К носит название постоянной Вина.

Из этого закона следует, что при повышении температуры АЧТ, максимум функции (или ) смещается в сторону коротких длин волн. (Отсюда и следует «странное» название – закон смещения.)

Развивая теорию теплового излучения, Джон Рэлей (1900г.) и Джеймс Джинс (1905г.) попытались получить аналитическую зависимость спектральной плотности энергетической светимости от частоты. Для этого они привлекли методы классической термодинамики. Т.к. в плоской электромагнитной волне энергия поровну распределяется между магнитным и электрическим полями, то можно считать, что каждой волне соответствует две степени свободы i =2, поэтому средняя тепловая энергия, переносимая электромагнитной волной, равна:

.

Подсчёт спектральной плотности количества волн (отношение возможного количества стоячих волн с частотами в интервале в некотором объёме к величине этого объёма) приводит к соотношению: . Следовательно, спектральная объемная плотность энергии равновесного теплового излучения будет равна: . Откуда для спектральной испускательной способности АЧТ (спектральной плотности энергетической светимости АЧТ) приходим к формуле Рэлея-Джинса: .

Оказалось, что формула Рэлея-Джинса удовлетворительно согласуется с экспериментальными данными об излучении абсолютно чёрного тела только в области больших длин волн (т.е. малых частот) и резко расходится с опытом для малых длин волн или больших частот излучения. При этом с ростом частоты объёмная плотность энергии неограниченно возрастает. Этот противоречивый результат, содержащийся в формуле Рэлея-Джинса, вывод которой с точки зрения классической теории не вызывал сомнений, П. Эренфест назвал «ультрафиолетовой катастрофой».

Гипотеза о квантах. Формула Планка.

«Ультрафиолетовая катастрофа» показала, что классическая физика содержит ряд принципиальных внутренних противоречий, которые проявились в теории теплового излучения и разрешить которые можно только с помощью принципиально новых физических идей.

Такая физическая идея была сформулирована Максом Планком в 1900 году в виде гипотезы о квантах. Согласно этой гипотезе энергия системы может принимать только дискретные значения. При испускании электромагнитных волн энергия системы уменьшается на величину энергии излучения. Поэтому энергия излучения тоже является дискретной. Минимальную величину энергии излучения он назвал квантом. Энергия кванта зависит от частоты излучения и определяется по формуле: .

Коэффициент пропорциональности Дж×с называется постоянной Планка. Соответственно, приведённая постоянная Планка Дж×с.

Постоянная Планка является принципиально новой константой и не может быть получена из констант классической физики.

Если рассмотреть равновесное излучение как термодинамическую систему, то к ней можно применить классическое распределение Больцмана. Вероятность нахождения системы в одном из состояний со значением энергии E_n определяется выражением:

,

где суммирование проводится по полному набору дискретных значений .

Среднее значение энергии определится выражением:

.

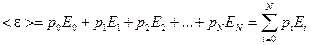Для электромагнитной волны теплового излучения характерно излучение во всём диапазоне частот, поэтому набор энергий будет бесконечным . Тогда

.

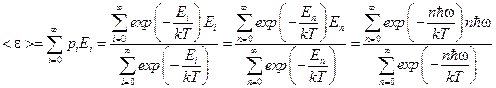Здесь для удобства немой индекс суммирования i заменён на n. Учтем, что в бесконечной геометрической прогрессии

1, , , , …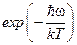

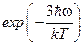знаменатель прогрессии равен 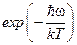. Если предположить, что , то сумма равна:

.

Тогда среднее значение энергии излучения с частотой определится из следующих преобразований:

,

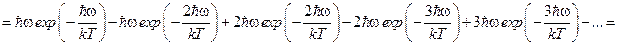
т.е. .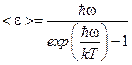

Следовательно, спектральная объёмная плотность энергии теплового излучения будет равна:

. Откуда .

Дата добавления: 2014-01-05