Вращение вокруг главных линий плоскости

Натуральная величина плоской фигуры может быть найдена вращением её вокруг горизонтали, фронтали или профильной прямой до положения, параллельного одной из плоскостей проекций.

Например, определим натуральную величину ΔАВС общего положения вращением его относительно горизонтали g (совпадающей с одной из сторон АС треугольника АВС) до положения горизонтального уровня (рис. 5.15). Вершины А и С треугольника АВС при вращении своего положения не меняют, т.к. точки А и С лежат на горизонтали g (на оси вращения). Следовательно, и проекции этих точек не изменят своего положения на комплексном чертеже. Точка В перемещается по дуге окружности радиусом r (ОВ), где точка О является центром вращения и определяется перпендикуляром восстановленным из точки В к оси вращения (g).

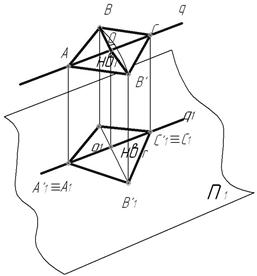
Рис. 5.15.

Вращение точки В происходит в плоскости перпендикулярной оси вращения g, а следовательно и изменение положения горизонтальной проекции В₁ будет осуществляться в этой же плоскости т.е. по прямой перпендикулярной к g₁ – В₁В^/₁. Тем самым определяется положение проекций центра вращения О₁, О₂ и проекций радиуса вращения r₁ (О₁В₁) и r₂ (О₂В₂). Откладывая расстояние О₁В^/₁ равное натуральной величине радиуса вращения r, т.к. когда точка В займёт нужное положение (ΔАВС // П₁) горизонтальная проекция радиуса вращения О₁В^/₁ будет равна его натуральной величине, которая может быть определена способом прямоугольного треугольника, найдем новое положение горизонтальной проекции В^/₁ точки В.

Дата добавления: 2014-01-05