Вращение вокруг следа плоскости, или совмещение

Совмещение - частный случай вращения геометрических элементов вокруг горизонтали или фронтали, когда осью вращения является горизонтальный или фронтальный следы плоскости.

При совмещении с плоскостью проекций геометрическая фигура отобразиться на ней в натуральную величину.

Покажем совмещение плоскости Р(Р₁,Р₂) с плоскостью П₁ (рис. 5.16). Так как горизонтальный след плоскоти Р₁ -ось вращения, то его положение и положение точки схода следов Р_Х не меняется. Для нахождения Р₂ в совмещённом положении на нём взята произвольная точка N (N₁, N₂) и найдено новое её положение, совмещённое с плоскостью проекций П₁.

Точка N при вращении перемещается в плоскости Q перпендикулярной оси вращения i º P₁ по дуге окружности радиуса r = ON.

Фронтальный след плоскости в совмещённом положении Р₂⁰ проводим через точки P_X и N⁰. При этом отрезок ON⁰ является натуральной величиной радиуса вращения r. На комплексном чертеже натуральная величина радиуса вращения найдена способом прямоугольного треугольника, практически же натуральная величина r - радиуса вращения точки N не определяют, т.к. отрезок [ P_XN₂ ] равен отрезку [ P_XN₂⁰ ]. Поэтому для нахождения точки N₂⁰ достаточно провести дугу радиуса P_XN₂ до пересечения с перпендикуляром из N₁ к P₁ (к оси вращения i).

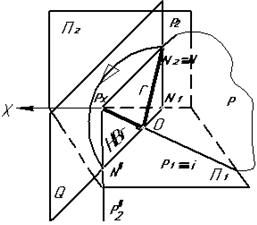
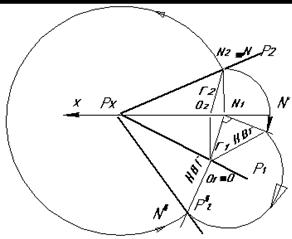
Рис. 5.16.

Покажем совмещение заданной плоскости Р(Р₁, Р₂) и принадлежащей ей некоторой точки А с горизонтальной плоскостью проекций П₁ (рис. 5.17). Для этого вначале найдём совмещённое с П₁ положение Р₂, а затем совмещенное положение g⁰ горизонтали g на которой находится точка А.

При совмещении плоскости Р(Р₁, Р₂) и принадлежащей ей точки А с фронтальной плоскостью проекций П₂ рекомендуется использовать фронталь f (рис. 5.18).

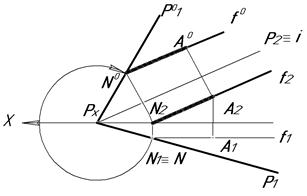
Рис. 5.17. Рис. 5.18.

Чтобы найти истинную величину плоской фигуры способом совмещения, нужно совместить с одной из плоскостей проекций ряд характерных точек её периметра.

На рис. 5.19 представлены комплексные чертежи плоскостей Р(Р₁, Р₂) частного положения (соответственно, две плоскости горизонтально проецирующего и две плоскости фронтально проецирующего положения) и принадлежащей ей точки А и их совмещение с плоскостями проекций П₁ и П₂.

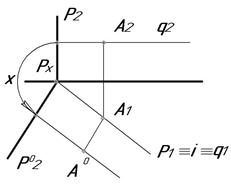
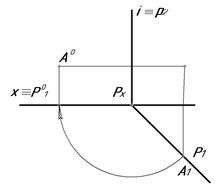
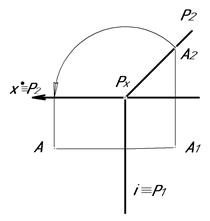
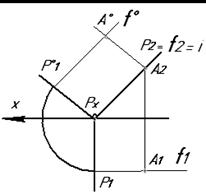
Рис. 5.19.

5.3. Пример выполнения графической работы «Преобразование проекций»

Даны координаты вершин пирамиды SАВС.

Требуется: определить двугранный угол при ребре SA – угол между смежными гранями пирамиды методом ЗПП.

Эта задачи решается на комплексном чертеже листа формата АЗ.

Исходные данные

Координаты точек (мм)
S	A	B	C
10,15,0	40,80,60	10,60,75	120,50,50

Числовые данные варианта взять из приложения 11.2. Номер варианта выдается преподавателем.

Оформление данной графической работы указано в прил. 11.1.

1) Выполнение построений на чертеже начинают с проработки соответствующей темы данного учебного пособия и лекционного материала.

2) По числовым значениям X и Z, X и Y координат точек вершин пирамиды строятся фронтальные и горизонтальные проекции граней пирамиды SАВ и SАС, показывая видимость их сторон.

Преобразование комплексного чертежа методом замены плоскостей проекций (ЗПП) осуществляется относительно линии пересечения двух плоскостей – ребра SA, которое является общим для двух пересекающихся граней (SАВ и SАС). Угол, образованный двумя плоскостями Р (Δ SАВ) и Q (Δ SАС), измеряется плоским углом γ, расположенным в плоскости перпендикулярной прямой SA, по которой пересекаются плоскости.

Мерой двухплоскостного (двугранного) угла служит линейный угол γ, образованный ортогональным проецированием его на плоскость, перпендикулярную к прямой SA, являющейся линией пересечения двух плоскостей P и Q (рис. 5.20).

В случае, приведенном на рис. 5.20, ребро SA двухплоскостного угла –

прямая общего положения. Поэтому для преобразования проекции угла так, чтобы его основание SA стало перпендикулярно к новой плоскости проекций, потребуется выполнить две замены плоскостей проекций (с переводом SA в положение уровня, а затем в проецирующее положение).

Сначала спроецируем угол на новую горизонтальную плоскость проекций П_4, перпендикулярную к плоскости П₁ и параллельную прямой пересечения SA. Новую ось проекций Х₂ проводим параллельно сохраняемой проекции S₂A₂. Для получения проекций треугольников SAB и SAC на плоскость П₄ опускаем из точек S₁, A₁, C₁ и B₁ перпендикуляры на ось Х₂ и откладываем от нее на продолжении этих перпендикуляров координаты " Z " точек S, A, B и C, беря их как расстояние проекций S₂. A₂, B₂ и C₂ до оси ОХ. Прямая пересечения SA двух плоскостей cпроецируется на П₄ в натуральную величину (S₄A₄ = SA).

Затем введем новую фронтальную плоскость проекций П_5, перпендикулярную к плоскости П₄ и прямой SA. Новую ось Х₃ системы плоскостей проекций П₄/П₅ проводим перпендикулярно к проекции S₄A₄. Прямая SA на плоскость П₅ проецируется в точку S₅ ≡ A₅. Построив проекции B₅ и C₅ точек C и B (расстояния точек A₅, S₅, B₅ и C₅ от оси Х₃ равны расстояниям точек A_{1 ,} S_{1 ,} B₁ и C₁ до оси Х₂), соединяем их прямыми с точкой S₅ ≡ A ₅. Линейный угол B₅S₅C₅ является величиной искомого двухплоскостного угла между плоскостями треугольников SАВ и SАС.

Как полученные, так и исходные данные следует отобразить в работе в виде таблиц произвольного размера, расположенных в свободном поле чертежа. Пример выполнения третьего задания графической работы приведен на рис. 5.20.

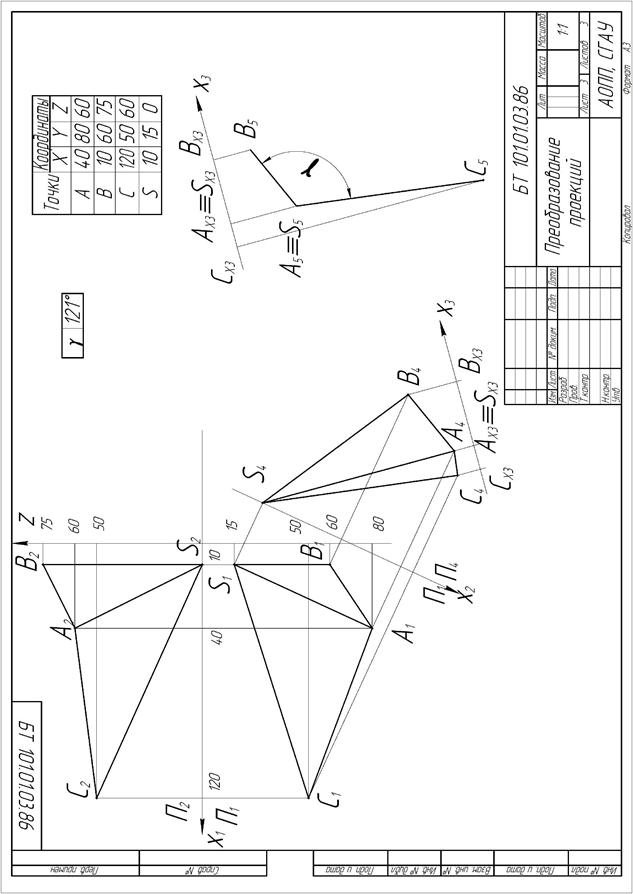
Рис. 5.20. Пример выполнения графической работы « Преобразование проекций ».

5.4 Пример выполнения графической работы «Пересечение плоскостей»

Даны две пересекающиеся плоскости Р и Q заданные треугольниками АВС и SЕD; координаты вершин треугольников А, В, С, S: Е и D определены при выполнении графической работы «Плоскости». Требуется:

1) по координатам точек вершин треугольников АВС и SЕD построить их фронтальные и горизонтальные проекции;

2) построить линию пересечения плоскостей;

3) определить угол пересечения плоскостей.

Эти задачи решаются на одном комплексных чертежах листа формата АЗ.

Исходные данные

Координаты точек (мм)
S	A	B	C	D	Е
10,15,0	30,60,20	10,30,58	90,20,38	52,85,75	0,93,55

Числовые данные варианта взять из приложения 11.2, и с графической работы «Плоскости». Номер варианта выдается преподавателем.

Оформление данной графической работы указано в прил. 11.1.

1) Выполнение построений на чертеже начинают с проработки соответствующей темы данного учебного пособия и лекционного материала.

2) По числовым значениям X и Z, X и Y координат точек вершин треугольников АВС и SЕD строятся их фронтальные и горизонтальные проекции. Одноименные проекции вершин соединяются прямыми линиями. Показывается видимость сторон треугольников, с помощью метода конкурирующих точек (п. 3.6).

3) Линию пересечения двух треугольников строят по точкам пересечения сторон одного треугольника с другим или по точкам пересечения каждой из сторон одного треугольника с другим. Линию пересечения можно также построить, используя вспомогательные секущие плоскости проецирующего положения - или положения уровня. Например, для определения линии пересечения треугольников АВС и SDЕ вводим вспомогательную плоскость горизонтального уровня R (на рис.5.21 показан ее фронтальный след R₂). Эта плоскость, пересекает треугольники в точках С,1, 2, 3, образуя две линии пересечения – С -1 и 2-3. Там, где пересеклись их горизонтальные проекции, отметили горизонтальную проекцию N₁ точки пересечения двух треугольников N, а поднявшись вверх по ЛПС до следа R₂ - фронтальную N₂. Вторую точку пересечения треугольников - М можно определить аналогично, введением еще одной вспомогательной плоскости уровня. В рассмотренном же примере (рис 5.21) вторую точку М определяли по точкам пересечения стороны DS треугольника SDE со сторонами СВ и АВ треугольника АВС. Фронтальная проекция стороны D₂S₂ пересекается с фронтальными проекциями сторон С₂В₂ и А₂В₂ в точках 4₂ и 5₂. А в пересечение горизонтальных проекций D₁S₁ и полученной прямой 4₁5₁ отметим горизонтальную проекцию точки М_{1 .}. Фронтальную проекцию М₂ отметим на стороне D2S2 по ЛПС от точки М₁. Соединив одноименные проекции точек M и N получим проекции линии пересечения двух треугольников М₁N₁ и М₂N₂.

4) Угол, образованный двумя плоскостями Р и Q измеряется плоским углом. расположенным в плоскости перпендикулярной прямой, по которой пересекаются плоскости. Рассмотрим определение натуральной величины угла между плоскостями, заданными треугольниками АВС и SЕD (рис.5.21).

Мерой двухплоскостного угла служит линейный угол, образованный ортогональным проецированием его на плоскость, перпендикулярную к прямой их пересечения МN (рис. 5.21).

Сначала проецируем угол на плоскость П₄ перпендикулярную к плоскости П₂ и параллельную прямой пересечения МN. Новую ось проекций Х₂ проводим параллельно сохраняемой проекции М₂N₂. Для получения проекций треугольников АВС и SЕD на плоскость П₄ опускаем из точек А₂ В₂ С₂ S₂ Е₂ D ₂, перпендикуляры на ось Х₂ и откладываем от нее на продолжении этих перпендикуляров координаты " Y " точек А, В, С, S, Е, D, беря их как расстояние от проекций А₁В₁С₁S₁Е₁ и D₁ до оси ОХ. Прямая пересечения МN двух плоскостей cпроецируется на П₄ в натуральную величину (М₄N₄=МN).

Вводим новую плоскость проекций П₅. перпендикулярную к плоскости П₄ и к прямой МN. Новую ось Х₃ системы плоскостей проекций П₄/П₅ проводим перпендикулярно к проекции М₄N₄. Прямая МN на плоскость П₅ спроецируется в точку М₅ ≡ N₅. Построив проекции А₅ В₅ С₅ S₅ Е₅ и D ₅ точек А, В, С, S, Е, D (расстояния точек М₅, N_б, К₅ и L₅ от оси Х₃ равны расстояниям точек М₂, N₂, К₂ и L₂ до оси Х₂), соединяем прямыми точки принадлежащие каждому из треугольников (отдельно точки А, В, С и точки S, D, E). При правильном построении две полученные проекции треугольников А₅В₅С₅ и S₅Е₅D₅ (прямые) пересекутся в точке М₅=N₅. Линейный угол А₅М₅S₅ является величиной искомого двухплоскостного угла между плоскостями треугольников АВС и SЕD.

Как полученные, так и исходные данные следует отобразить в работе в виде таблиц произвольного размера, расположенных в свободном поле чертежа. Пример выполнения третьего задания графической работы представлен на рис. 5.21.

Дата добавления: 2014-01-05