Случайные ходы

Лекция №14-15. Случайные ходы и лотереи.

Цель: изучить особенности решения лотерей и игр со случайными ходами.

Ключевые слова: случайный ход, лотерея.

Вопросы:

1. Случайные ходы.

2. Понятие лотереи.

Имеется еще один источник неопределенности игроков относительно состояния позиции - случай. Например, в карточных играх игроки обычно не знают карты партнеров (недаром их тщательно перетасо­вывают перед раздачей), и это тоже нужно отразить в описании игры. Одна­ко, в отличие от предыдущей неопределенности, эта неопределенность носит вероятностный характер и имплантируется сравнительно легко. Формально просто к списку игроков добавляется фиктивный игрок - природа, которая тоже выбирает свои ходы, но делает это не свободно, как обычные игроки, а с предписанными вероятностями.

Для примера рассмотрим следующую пародию на ’’покер”. Первый игрок (Ваня) получает карту, которая в 1/6 случаев благоприятна для него. По­смотрев карту, он может либо ’’повысить ставку” (Д), либо ’’спасовать” (Р). Во втором случае игра заканчивается, и Ваня отдает второму игроку (Маше) 10 р. В первом случае Маша, не видя карты, может либо ’’принять повыше­ние” (г), либо тоже ’’спасовать” (р). Выигрыши Вани (так как игра с нулевой суммой) в различных ситуациях приведены на рисунке ниже.

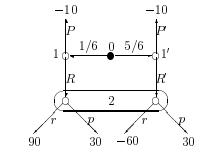Здесь у Вани два информационных множества 1 и 1; а у Маши - одно (так как она не видит карту).

Можно ли по такой игре образовать нормальную форму? Со стратегиями особых проблем нет. Снова каждый игрок должен решить, как он ведет се­бя (какой ход выбирает) в каждом своем информационном множестве. Ваня должен решить - что он делает при хорошей карте (в позиции 1) и что – при плохой, в позиции V. Так что у него 4 стратегии: RR\ RP'7 PR' и РР'. У Маши - две стратегии: г и р.

А вот с выигрышами возникает некоторая проблема. Допустим, Ваня вы­брал стратегию RR', а Маша - г. Если карта хорошая, Ваня получает 90 р., если плохая - теряет 60 р. Как же оценить его выигрыш? Простейший выход - посчитать математическое ожидание 90 • 1/6 — 60 • 5/6 = —35. Аналогично можно заполнить остальные клеточки.

Дата добавления: 2014-01-05