Пример.6.1

Пусть перед нами стоит задача интерпретации значений ЛП «возраст», таких как «молодой» возраст, «преклонный» возраст или «переходный» возраст. Определим «возраст» как ЛП (рис.6.1.). Тогда «молодой», «преклонный», «переходный» будут значениями этой лингвистической переменной. Более полно базовый набор значений ЛП «возраст» следующий:

В – {младенческий, детский, юный, молодой, зрелый, преклонный, старческий}.

Для ЛП «возраст» базовая шкала – это числовая шкала от 0 до 120, обозначающая количество прожитых лет, а функция принадлежности определяет, насколько мы уверены в том, что данное количество лет можно отнести к данной категории возраста (от 0 до 1). На рис.6.2 отражено, как одни и те же значения базовой шкалы могут участвовать в определении различных НМ.

Рис. 6.1. Лингвистическая переменная «возраст» и нечеткие множества, определяющие ее значения

Например, определить значение НМ «младенческий возраст» можно так:

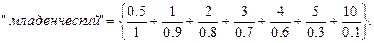
Рис. 6.2. Формирование нечетких множеств

Рис.6.3 иллюстрирует оценку НМ неким усредненным экспертом, который ребенка до полугода с высокой степенью уверенности относит к младенцам (m=1). Дети до четырех лет причисляются к младенцам тоже, но с меньшей степенью уверенности (0.5<m<0.9), а в десять лет ребенка называют так только в очень редких случаях – к примеру, для девяностолетней бабушки и 15 лет может считаться младенчеством. Таким образом, нечеткие множества позволяют при определении понятия учитывать субъективные мнения отдельных индивидуумов.

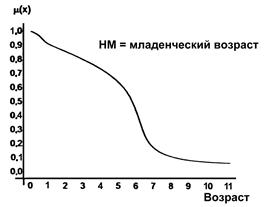
Рис. 6.3. График функции принадлежности нечеткому множеству «младенческий возраст».

Дата добавления: 2014-01-05