Нечеткие правила вывода

Базовое правило вывода типа "если - то" (англ.: if- then rule) называется также нечеткой импликацией, принимающей форму

если х это А, то у это В (6.1)

где А и В - это лингвистические значения, идентифицированные нечетким способом через соответствующие функции принадлежности для переменных х и у. Часть "х это А" называется условием (предпосылкой), а "у это В" - следствием (заключением). Импликацию (6.1) можно записать в сокращенном виде А → В. Нечеткое рассуждение - это процедура, которая позволяет определить заключение, вытекающее из множества правил "если - то". Такое множество при N переменных х может принять вид

если x₁ это А₁ и х₂ это А₂ и... и x_N это A_N, тo у это В (6.2)

Переменные x₁, x₂, …, x_N образуют N -мерный входной вектор x, составля­ющий аргумент условия, в котором А₁, А₂ ,..., A_n и В обозначают величины соответствующего коэффициента принадлежности , . Необходимо обратить внимание, что здесь присутствуют индивидуальные функции принадлежности для каждой переменной х_i, и отдельно для y. Случайное значение функции принадлежности 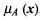, где х - это вектор х = [ x₁, x₂, …, x_N ] отно­сящееся к условию импликации (уровень активации правила), должно в последующем интерпретироваться с использованием введенных ранее нечетких операций. Возможна интерпретация (то есть определение уровня активации (нечеткого значения) переменной, указанной в следствии правила) в форме логического произве­дения множеств либо в форме алгебраического произведения:

1. интерпретация в форме логического произведения (из всех нечетких значений переменных условия правила берется минимальное):

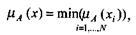(6.3)

2. интерпретация в форме алгебраического произведения (в качестве нечеткого значения переменной следствия правила берется значение, полученное путем перемножения нечетких значений переменных условия правила):

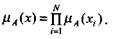(6.4)

Приписывание единственного значения функции принадлежности, описы­вающей многомерное условие, будем называть агрегированием предпосылки. Каждой импликации А → В, определенной выражением (6.2), можно приписать также единственное значение функции принадлежности . Наиболее популярные интерпретации этой функции также имеют форму логического или алгебраического произведения:

· форма логического произведения

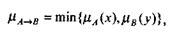(6.5)

· форма алгебраического произведения

(6.6)

Приписывание единственного значения функции принадлежности всей импликации будем называть процедурой агрегирования на уровне импликации.

Дата добавления: 2014-01-05