Условия уравновешенности ротора

Деталь, вращающаяся в опорах, называется ротором. В связи с появлением быстроходных машин возникла проблема уравновешивания быстровращающихся деталей. Так, например, скорость некоторых турбин, валов гироскопов, суперцентрифуг достигает 3-50 тысяч об/мин и малейшее смещение центра масс с геометрической оси вращения вызывает появление больших сил инерции, т.е. вибрационных явлений в машине и фундаменте.

При вращении какой-либо i -й массы m на нее действует сила инерции, которую можно разложить на нормальную 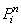и тангенциальную 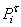составляющие (рис. 6.1).

Величины этих сил можно вычислить по формулам

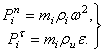(1)

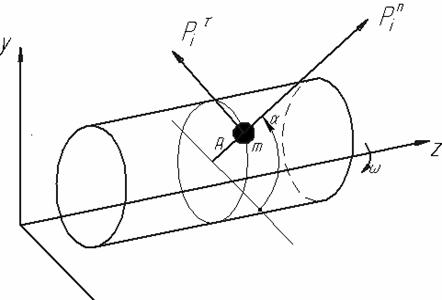
Рис. 6.1. Схема ротора

Спроектируем эти силы на оси х, у, z и определим моменты этих сил относительно осей:

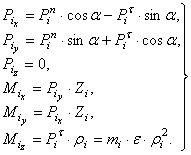(2)

Подставив (1) в (2) и просуммировав, получим (учитывая, что ,)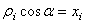

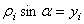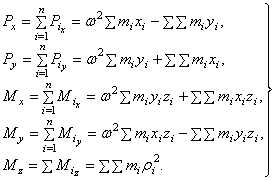
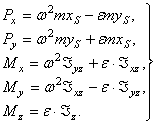(3)

Последнее уравнение в (3) можно исключить, так как момент 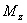не создает дополнительной реакции в опорах ротора.

Силы 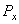и 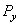, моменты 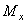и 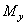равны нулю в том случае, если координаты x и y массы m расположены на оси вращения z (т.е. центр масс ротора неподвижен):

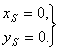(4)

Это есть условие статической уравновешенности ротора.

Моменты 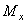и 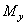равны нулю, если центробежные моменты инерции ротора равны нулю:

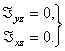(5)

Это есть условие динамической уравновешенности ротора.

Такое уравновешивание применяется для плоских деталей, длина которых мала по сравнению с диаметром.

Выводы: ротор статически уравновешен, если его центр тяжести расположен на оси вращения; ротор динамически уравновешен, если его ось вращения является главной центральной осью инерции.

Уравновешенность ротора можно охарактеризовать и силовыми параметрами. Он статически уравновешен, если главный вектор сил индукции 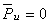. Ротор динамически уравновешен, если главный вектор моментов сил инерции .

При проектировании роторов используют условия (4) и (5). При проверке уравновешенности изготовленных роторов используют условия 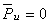и . Устранение остаточной неуравновешенности уже изготовленного ротора, возникшей по причинам неточности изготовления, монтажа, из-за неоднородности материала, из которого изготовлен ротор, называется балансировкой. Балансировка вращающихся масс осуществляется на специальных балансировочных станках, при этом исключается неуравновешенность, вызванная неточностью изготовления детали. Техника статической и динамической балансировки жестких роторов входит в содержание лабораторного практикума по дисциплине «Теория механизмов и машин».

Дата добавления: 2014-01-05