Уравновешивание масс, находящихся в одной плоскости

Уравновешивание вращающихся масс

Положения отдельных неуравновешенных масс 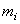, расположенных на роторе, можно охарактеризовать величинами радиус-векторов относительно оси его вращения. Система вращающихся масс будет уравновешена, если главный вектор сил инерции, действующих на эти массы при их совместном вращении, равен нулю:

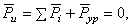
где – сила инерции, действующая на i-ю массу; 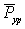– сила инерции уравновешивающей массы 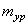, расположенной на расстоянии от оси вращения ротора.

Сила инерции, действующая на i -ю массу, вращающуюся с постоянной скоростью 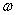, равна .

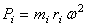Рассмотрим систему, состоящую из трех неуравновешенных вращающихся масс m₁, m₂ и m₃ (рис. 6.2).

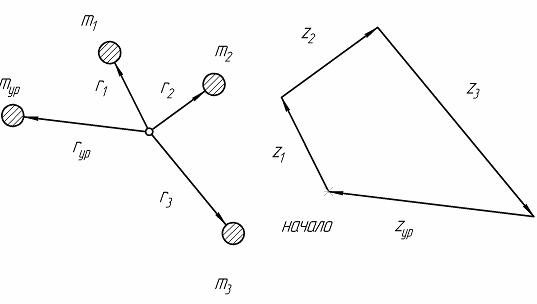
а) б)

Рис. 6.2. Система неуравновешенных масс (а) и план сил инерции (б)

Условием уравновешенности данной системы масс является уравнение

.

Так как 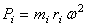, то это уравнение можно записать в виде

Так как (мы рассматриваем вращающуюся систему масс), то

. (6)

Уравнение (6) можно решить аналитическим и графическим методами.

При аналитическом методе решения составляются уравнения проекций сил на координатные оси, из которых находят являющееся неизвестным последнее слагаемое.

Найдем и графическим методом, то есть построением векторного многоугольника (см. рис. 6.2, б), являющегося графической интерпретацией векторного уравнения (6). Предварительно выбираем масштаб сил

,

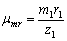где z ₁ – длина вектора, изображающего силу 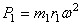, (мм).

Размерность масштаба 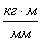(если масса задана в кг, радиус – в м).

Переведем масштабом 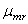другие известные слагаемые уравнения (6) в векторные отрезки:

Тогда векторное уравнение (6) запишется в виде

.

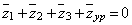Построив векторный силовой многоугольник (см. рис. 6.2, б) в масштабе 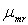, из него определим длину вектора 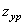. Выбрав из конструктивных соображений величину , вычисляем уравновешивающую массу

.

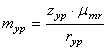Поместив ее на роторе в направлении вектора на расстоянии от оси вращения, равном длине этого вектора, уравновесим ротор.

На практике наиболее часто статическое уравновешивание проводят:

- выбирая симметричные схемы механизма;

- устанавливая на звеньях механизма противовесы (или корректирующие массы);

- размещая противовесы на дополнительных звеньях или кинематических цепях.

Дата добавления: 2014-01-05