Пример 1. Рассмотрим язык L, состоящий из всех слов в алфавите Σ = {a, b}, которые начинаются на aa и содержат нечетное число символов b

Рассмотрим язык L, состоящий из всех слов в алфавите Σ = {a, b}, которые начинаются на aa и содержат нечетное число символов b.

Для выделения слов, начинающихся на aa создадим начальное состояние q₀, которое первый символ a будет переводить в состояние q₁, а второй символ a будет переводить q₁ в состояние q₂. Ясно, что все слова, которые начинаются на ab, ba, bb сами не входят в язык L и все их продолжения также ошибочны. Заведем для них ошибочное состояние q_!. Остальные слова естественно разбиваются на два класса: т.е., в которых четное число символов b, и те, в которых число таких символов нечетно (они и принадлежат L). Так как после получения aa число b четно, то для представления слов первого класса будем использовать состояние q₂, а для представления слов второго создадим состояние q₃, которое и будет заключительным. В результате получаем автомат, диаграмма которого представлена на рис. 5.14. Здесь начальное состояние отмечено стрелкой 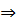, а заключительное состояние отмечено двумя окружностями.

Рис. 5.14. Диаграмма автомата А

Проверим работу этого автомата, например, на входном слове w = aaababa. При его чтении порождается следующая последовательность конфигураций:

(q₀, aaababa) (q₁, aababa) ((q₂, ababa) 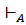((q₂, baba) 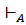((q₃, aba) 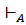((q₃, ba) 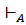((q₂, a 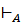()(q₂, ε).

Заключительное состояние этого вычисления q₂ не является заключительным.

Следовательно, w 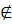L_A. Если же мы рассмотрим в качестве входа слово w₁= wb =aaababab, то, продолжив на один шаг приведенное выше вычисление, получим, что (q₀, w₁) 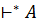(q₃, ε). Следовательно, w₁ L_A.

Проверка показала, что на двух входах автомат A работает верно. Как установить, что он построен корректно, т.е. верно работает на всех входных словах и распознает L?

Дата добавления: 2014-01-05