Произведение автоматов

Схема доказательства правильности конечного автомата

Схема доказательства правильности конечного автомата такова:

1) определить (описать) для каждого состояния q Q язык L(q),состоящий из слов, переводящих начальное состояние q₀ в q;

2) доказать, что это определение правильное, используя индукцию по длине входного слова;

3) показать, что .

Применим эту схему к доказательству правильности, построенного выше автомата A. Языки, связанные с состояниями этого автомата, фактически, уже были определены при его построении. Уточним их:

L(q₀) = {ε},

L(q₁) = {a},

L(q₂) = {w | слова, начинающиеся с aa и содержащие четное число букв b},

L(q₃) = L,

L(q_!) = {w | слова, не начинающиеся с aa}.

Правильность определения языков L(q₀), L(q₁) и L(q₁) следует непосредственно из определения A. Самое короткое слово, переводящее q₀ в q₂aa, и оно принадлежит L(q₂). Аналогично, самое короткое слово, переводящее q₀ в q₃ aab, и оно принадлежит L(q₃). Предположим теперь, что для каждого слова w длины ≤ n выполнено условие (*):

Покажем, что оно будет выполнено и для всех слов длины n + 1.

Пусть |w|=n+1. Тогда w=w^’α, где α {a, b}. Так как |w^’| = n, то для w^’ выполнено условие (*). Поэтому, если w’ переводит q₀ в q₂, то это слово начинается с aa и содержит четное число b. При α = a слово w переводит q₀ в q₂ и также начинается с aa и содержит четное число b, а при α = b слово w переводит q₀ в q₃, начинается с aa и содержит нечетное число b, т.е. принадлежит L.

Аналогично, если w’ переводит q₀ в q₃, то это слово начинается с aa и содержит нечетное число b. При α =a слово w также переводит q₀ в q₃ и также начинается с aa и содержит нечетное число b, а при α = b w переводит q₀ в q₂, оно начинается с aa и содержит четное число b. Обратно, если α= a, то слово w переводит q₀ в q_i (i = 2, 3) 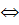w^’ переводит q₀ в q_i(i = 2, 3) и условие (*) выполнено, так как четность числа букв b в w и в w’ одинакова. Если же α = b, то из определения автомата A следует, что слово w переводит q₀ в q₂ 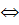w’ переводит q₀ в q₃ и w переводит q₀ в q₃ 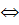w ^’переводит q₀ в q₂. Так как четность числа букв b в w и в w⁰ разная, то и в этом случае условие (*) выполнено. Для завершения доказательства осталось заметить, что единственным заключительным состоянием автомата A является q₃ и поэтому L_A= L(q₃) = L.

Рассмотрим одну важную конструкцию конечного автомата по двум другим, называемую произведением автоматов, которая позволит установить замкнутость класса конечно автоматных языков относительно теоретико множественных операций.

Пусть M₁=< Σ, Q₁, 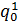^{, ,}Φ₁> и M₂=< Σ, Q₂, 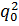_{, F}2^,Φ₂> два конечных автомата с общим входным алфавитом Σ, распознающие языки L₁ и L₂, соответственно.

Определим по ним автомат M=< Σ, Q, q₀, F, Φ >, называемый произведением M₁ и M₂(M = M₁хM₂), следующим образом. Q = Q₁хQ₂= {(q, p) | q Q₁, p Q₂}, т.е. состояния нового автомата это пары, первый элемент которых состояние первого автомата, а второй состояние второго автомата. Для каждой такой пары (q, p) и входного символа a 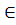Σ определим функцию переходов: Φ((q, p), a) =(Φ₁(q, a), Φ₂(p, a)). Начальным состоянием M является пара q₀= ( 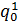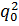_, ), состоящая из начальных состояний автоматов-множителей. Что касается множества заключительных состояний, то оно определяется в зависимости от операции над языками L₁ и L₂, которую должен реализовать M.

Дата добавления: 2014-01-05