Детерминизация НКА

Детерминированные конечные автоматы являются частными случаями недетерминированных. Следовательно возникает вопрос, распознают ли недетерминированные конечные автоматы больший класс языков чем детерминированные? На данный вопрос отвечает теорема показывает, что классы языков, распознаваемых НКА и ДКА совпадают.

Теорема 1. Детерминизация НКА

Для каждого НКА M можно эффективно построить такой ДКА A, что L_A= L_M.

Доказательство. Пусть M =< Σ, Q, q₀, F, Φ > НКА. Процедура построения по нему эквивалентного ДКА состоит из двух этапов: на первом построится эквивалентный ему НКА M₁, в программе которого отсутствуют переходы по ε, а на втором этапе по M₁ строится эквивалентный ДКА A.

Этап 1. Устранение пустых переходов.

Рассмотрим поддиаграмму автомата M, в которой оставлены лишь ребра, помеченные ε:Dε^{= (}Q, Eε⁾, где Eε⁼{(q, q^’)|q^’ Φ(q, ε)}. Пусть 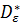^{= (}Q, 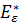₎ - это граф достижимости (транзитивного замыкания) для Dε. Тогда 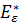₌{(q, q^’) |q = q’ или в Dε имеется путь из q в q’}.

Определим НКА M₁=< Σ, Q₁, q₀, F₁, Φ₁> следующим образом:

Q₁= {q₀} {q| существуют такие q’Q и aΣ, что q Φ(q’0, a)}, т.е. кроме начального остаются лишь те состояния, в которые входят непустые ребра.

F₁= {q| существует такое q^’F, что (q, q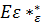^’) _}, т.е. к заключительным состояниям M добавляются состояния, из которых можно было попасть в заключительные по путям из ε -ребер.

Для каждой пары q^’Q, a 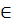Σ полагаем

Φ₁(q, a) ={r| существует такое q^’F, что (q, q^’) Eε∗_иr Φ(, q^’, a)}, т.е. в 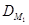имеется a-ребро из q в r, если в D_M был (возможно пустой) путь из ε -ребер в некоторое состояние q^’, из которого a -ребро шло в r.

Из этого определения непосредственно следует, что в НКА M₁ нет пустых переходов по ε. Установим эквивалентность M и M₁.

Лемма 1. .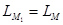

Доказательство. Пусть w=w₁w₂...w_t произвольное входное слово. Предположим, что w 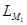. Это означает, что в диаграмме 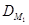имеется путь p = e₁e₂... e_t(e₁= (q₀=r₀, r₁), 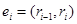i= 2,..., t) из q₀ в некоторое состояние 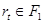, который несет слово w, т.е. ребро e_i помечено символом w _i. Из определения функции Φ₁ непосредственно следует, что для любого ребра 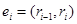этого пути в диаграмме D_M имеется путь из 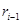в r_i, начало (возможно пустое) которого состоит из ε -ребер, а последнее ребро помечено символом w_i. Объединив эти пути, получим в диаграмме D_M путь из q₀ в r_t, который несет слово w. Так как r_t 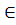F₁, то либо r_t 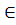F, либо в D_M имеется путь по ε-ребрам из r_t в некоторое состояние r’ 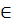F. В обоих случаях в D_M имеется путь из q₀ в заключительное состояние, который несет слово w, и следовательно w L_M.

Обратно, пусть w L_M. Тогда в D_M имеется путь из q₀ в некоторое заключительное состояние r, который несет слово w. Пусть r₀=q₀, а r_i - это состояние этого пути, в которое приводит ребро с меткой w_i(i = 1,..., t). Рассмотрим отрезок этого пути между вершинами r_i−1 и r_i. Последнее ребро этого отрезка имеет метку w_i, а все предыдущие (если они имеются) помечены ε. Тогда по определению Φ₁ в диаграмме 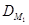между r_i−1 и r_i имеется ребро с меткой w_i. Объединив эти ребра, получим в 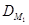путь из q₀ в r_t. Так как либо r_t= r F, либо в D_M из r_t имеется путь из ε- ребер в r F, то из определения F₁ следует, что r_t 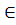F₁. Таким образом, w .

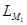Этап 2. Детерминизация.

Идея детерминизации состоит в том, что состояниями ДКА объявляются подмножества состояний НКА. Тогда для каждого такого подмножества T и входного символа a однозначно определено множество состояний T^’, в которые НКА может попасть из состояний T при чтении a.

Определим по НКА M₁=< Σ, Q₁, q₀, F₁, Φ₁> ДКА A=<Σ,Q^А, 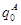F^A,Φ^A> следующим образом.

Q^A= {Q^’| Q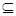^’ Q₁},

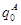= {q₀},

F^A= {Q^’| Q^’∩ F₁ ∅},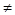

Φ^A(Q^’, a) = {q | существует такое q^’ Q^’, что q Φ₁(q^’, a)}.

Ясно, что A детерминированный конечный автомат. Следующая лемма устанавливает связь между его вычислениями и вычислениями исходного НКА.

Лемма 2. Для любой пары состояний Q^’, Q^’’ из Q^’ и любого слова w 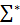имеем (Q^’, w) 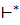_A(Q^’’, ε)⇐⇒Q^’’= {r | существует такое q^’Q^’, что (q, w) 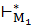⁽r, ε)}.

Доказательство. Применим индукцию по длине слова w.

Базис. Пусть |w| = 0, тогда w = ε, Q’= Q’ ’ и утверждение выполнено. Пусть теперь |w| = 1 и w = a Σ. Тогда утверждение леммы следует непосредственно из определения Φ^A(Q^’, a).

Шаг индукции. Предположим, что лемма справедлива для всех слов длины ≤ k, и пусть |w| = k + 1. Выделим в w первый символ: w = aw^’. Пусть 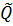- это такое состояние, что (Q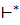^’, a) _A ( 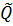, ε). Тогда ( 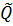, w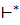^’) _A(Q^’’, ε). Так как |w^’| = k, то по индукционному предположению это эквивалентно тому, что Q’’= {r существует такое q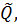^’ что (q, w’) 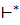_M1⁽r, ε)}. Но из определения Φ^A следует, что 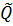= {q | существует такое q^’ Q^’, что q Φ₁(q^’, a)}. Объединив, эти два равенства получаем, что Q^’’= {r | существует такое q^’ Q’, что (q, w) 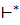_M1⁽r, ε)}.

Для завершения доказательства теоремы покажем с помощью леммы 2, что .

Действительно, если слово w переводит состояние q₀ в некоторое q F₁ автомате М₁,то положив в лемме 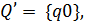получим, что 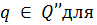состояния 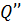, такого что 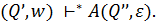Но тогда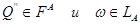

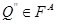Обратно, если w L_A, то для некоторого имеем ({q₀}, w) 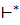_A(Q’’, ε). Тогда в Q^’’ имеется некоторое состояние q 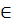F₁ и по лемме 2 в автомате M₁ (q₀, w) 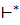_M1 ⁽q, ε)}, т.е. w .

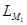Дата добавления: 2014-01-05