Расчет количественных показателей надежности систем при параллельном соединении их элементов

При последовательным соединением элементов по надежности, надежность системы может быть повышена путем увеличения надежности каждого элемента и путем уменьшения их числа.

При последовательным соединением элементов по надежности, надежность системы зависит от уровня надежности каждого элемента и от их числа. С уменьшением надежности элементов и увеличении их числа надежность системы уменьшается.

Рассмотрим соотношения, при помощи которых рассчитываются показатели надежности восстанавливаемых систем при параллельном соединении их элементов. Для этого необходимо использовать основное правило теории вероятности №5.

Правило №5. Вероятность появления любого одного события А₁ или А₂ или А₃ или … Аn из N несовместных событий равна сумма вероятностей этих событий:

Р(А₁ или А₂ или А₃ или … Аn) =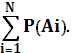

Для системы, состоящей из n параллельно соединенных элементов при экспоненциальном законе распределения времени до отказа:

P_c(t) = 1 - Q_c(t) = 1 - = 1 - ^-λi·t) - вероятность безотказной работы системы.

Использование данного правила позволяет получить основные соотношения для определения характеристик надежности систем при параллельном соединении элементов.

Q_c(t) = 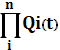= 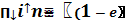^-λi·t) - вероятность отказа системы.

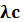= t^(n-1)· 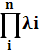- интенсивность отказов системы.

Т_с = 1 / 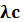- среднее время наработки до отказа системы.

К_гс(t) = 1 -- функция готовности системы.

К_гс = 1 -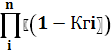 – коэффициент готовности системы.

К_гос(t, х) = 1 -- функция оперативной готовности системы.

К_гос(х) = 1 -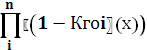 – коэффициент оперативной готовности системы.

μ_тс = 1 / 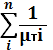- математическое ожидание наработки системы до отказа.

Рассмотрение соотношений для расчета количественных показателей надежности восстанавливаемых систем, состоящих из параллельно соединенных элементов, позволяет сделать следующие выводы:

Выводы:

Дата добавления: 2014-01-05