План лекции. 1. Длительность обслуживания заявок

1. Длительность обслуживания заявок

2. Характеристики процессов в СМО

1. Длительность обслуживания заявок.

Длительность обслуживания заявки на обработку данных в КСА определяется временем, необходимым процессору для исполнения соответствующей программы или совокупности программ, реализующих задачу обработки данных. В общем случае длительность обслуживания — случайная величина t_об с определенным законом распределения, различным для различных типов заявок. Предполагается, что длительности обслуживания различных последовательно исполняемых заявок независимы. Степень случайности длительности обслуживания зависит от степени разветвленности программы и от степени разнообразия исходных данных.

Пусть плотность распределения длительности обслуживания описывается произвольным законом распределения ft_об(t) с математическим ожиданием М [t_об] = 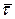_об. Для исследования и описания процессов в СМО необходимо иметь функцию ft_об(t) в аналитическом виде. С этой целью функция ft_об(t), если она найдена экспериментально, аппроксимируется некоторым типовым законом распределения.

В случае, когда из характеристик длительности обслуживания известно только математическое ожидание 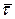_об, вероятностные свойства t_об аппроксимируются показательным распределением

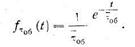
Такая аппроксимация оказывается справедливой в случае, когда программа, исполняемая по заявке, имеет большое число разветвлений различной протяженности, причем вероятность развития процесса по коротким ветвям больше, чем более протяженным.

Оказывается, что ряд аналитических зависимостей для процессов в СМО может быть получен для произвольного закона-, распределения длительности обслуживания заявок, относительно которого известны две его характеристики: математическое ожидание 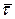_об и второй начальный момент 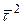_об. Именно такое допущение будет использоваться ниже при анализе дисциплин обслуживания заявок.

2. Характеристики процессов в СМО.

СМО типа М | М | 1 представляет разомкнутую одноканальную систему массового обслуживания с «чистым» ожиданием,. т.е. с неограниченной длиной очереди. На вход системы по­ступает простейший поток заявок. Пусть его интенсивность равна, l заявок в секунду. Время обслуживания t_об распределено по показательному закону со средним значением .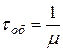

Процессы обслуживания в рассматриваемой СМО характеризуются следующими величинами:

— вероятностью р{п), п = 0, 1, 2, что в системе находится ровно п заявок;

— средним числом заявок, находящихся в очереди (п_оч), на обслуживании (п_об) и в целом в системе (п);

— средними значениями времени ожидания 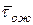, времени обслуживания , времени пребывания .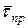

Представляет интерес среднее значение случайной величины

n _о6 = п — n _оч,

т. е. среднее значение числа заявок, находящихся на обслуживании. Эта случайная величина принимает значения 0 и 1 с вероятностями

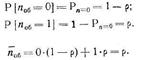
где 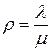- загрузка системы.

Таким образом, среднее число заявок, находящихся в СМО М | М |1 на обслуживании, численно равно загрузке r.

Система М | G |1 представляет собой одноканальную СМО с пуассоновским входным потоком и произвольным (общим) распределением времени обслуживания. Считаются заданными следующие параметры системы:

— интенсивность l входного пуассоновского потока заявок:

— математическое ожидание 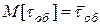и второй начальный момент 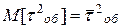времени обслуживания.

Таким образом, сам закон распределения времени обслуживания предполагается неизвестным.

Центральным вопросом исследования свойств СМО М | G \ 1 является определение среднего времени ожидания 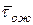по характеристикам 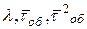. В основе решения задачи лежит анализ свойств случайной величины Y — оставшегося времени обслуживания заявки, уже находящейся на обслуживании, на момент прихода в систему новой заявки.

Пусть в канале СМО протекает процесс обслуживания заявок со средним временем обслуживания . В произвольный момент времени t_n на вход СМО поступает заявка z_n и застает канал СМО занятым обслуживанием некоторой заявки z_i i<n, поступившей ранее. Спрашивается, чему должно быть равно среднее время дообслуживания заявки z_i? На первый взгляд кажется, что среднее время дообслуживания должно бить равно /2. Оказывается такой ответ неверен. Предположим, что время обслуживания распределено по показательному закону со средним значением . Благодаря свойству от­сутствия последействия, время дообслуживания заявки z_i, застигнутой на обслуживании заявкой z_n, не зависит от того, сколько времени уже протекает обслуживание z_i и распреде­лено так же, как и полная длительность ее обслуживания. В этом случае среднее время дообслуживания заявки z_i будет равно среднему времени ее обслуживания , а не 0,5 !

Объяснение полученного парадокса состоит в том, что вероятности встречи заявки z_n с другими заявками в интервале их обслуживания в канале СМО неравнозначны. Ясно, что у нлямкн z_n больше шансов застать на обслуживании в СМО м.чяику z_i, имеющую «большую» длительность обслуживания.

Поэтому закон распределения длительности времени обслуживания заявки z_i застигаемой заявкой z_n оказывается отличным от закона распределения случайной величины .

Интервал времени обслуживания заявки z_i застигаемой на обслуживании заявкой z_n назовем «отобранным интервалом». Введем понятия длительность жизни Т, возраста Т_о и остаточного времени жизни Y отобранного интервала (рис. 1).

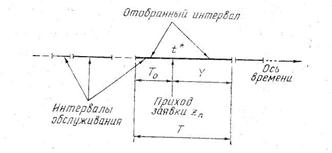
Рис. 1

Отобранный интервал описывается выражением:

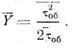
Таким образом, среднее значение Y остаточного времени численно равно второму начальному моменту 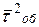времени обслуживания, деленному на удвоенное среднее значение времени обслуживания.

Выражение для среднего времени ожидания заявки в очереди, в общем случае, представляет сумму:

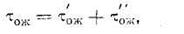
где 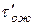— время ожидания завершения обслуживания некоторой заявки z_i уже находящейся на обслуживании в момент прихода заявки z_n

— время ожидания обслуживания всех заявок, находящихся в очереди к моменту прихода заявки z _п.

Выполним операцию математического ожидания:

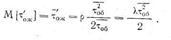
Диаграмма характеристик СМО М | G \ 1:

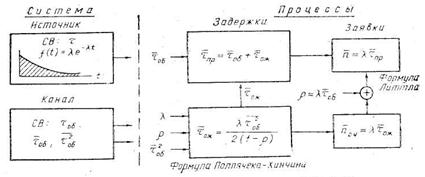
Рис. 2

Контрольные вопросы:

1. Какова длительность обслуживания заявок?
2. Чем характеризуются системы массового обслуживания?
3. Какими свойствами обладает простейший поток заявок?

Тема № 3 «Модели и свойства элементарных систем массового обслуживания»

Лекция № 8 «Характеристики дисциплин обслуживания заявок»

Цель лекции.

а) учебная цель:

Целью является формирование у слушателей целостного представления о принципах применения элементов теории вероятностей при моделировании сетевых процессов – элемента систем массового обслуживания.

Дата добавления: 2014-01-05