План лекции. 1. Модель системы обслуживания

1. Модель системы обслуживания

2. Характеристики процессов обслуживания

3. Характеристики дисциплин обслуживания

1. Модель системы обслуживания.

Схема системы обработки данных как СМО приведена на рис. 1. Предполагается, что источник заявок генерирует многомерный поток заявок, состоящий из заявок типа 1, 2,..., М. Поток заявок каждого типа простейший, с интенсивностью l.

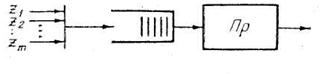
Рис.1

Управление обработкой заявок производится следующим образом. При поступлении очередной заявки на вход системы программа—диспетчер инициирует прерывание в процессоре, в результате которого запускается программа приема и постановки заявки в соответствующую очередь O_i на исполне­ние заявки. Физически каждая очередь О _i состоит из совокупности ячеек оперативной памяти процессора, в которых размещаются данные (коды) поступающих заявок. Отбор заявок на обслуживание из очередей O_i производится программой-диспетчером в порядке поступления заявок.

Пусть на вход системы поступают М пуассоновских потоков заявок с интенсивностями 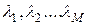На входе системы из этих потоков формируется один суммарный поток с интенсивностью:

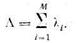
Свойства канала обслуживания (т. е. процессора и соответствующей обрабатывающей программы) описываются двумя наборами характеристик:

1) величиной среднего времени обслуживания заявки типа i

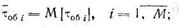
2) величиной второго начального момента времени обслуживания заявки i -го типа:

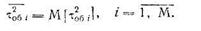
Таким образом, модель рассматриваемой системы обслуживания полностью описывается набором параметров 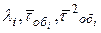для i = 1…M. Эти характеристики указаны в левой части; диаграммы рис. 2.

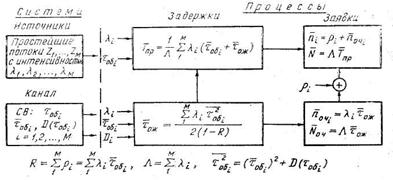
Рис. 2.

2. Характеристики процессов обслуживания.

К характеристикам процесса обслуживания относятся суммарная загрузка системы, средние значения: времени ожидания в очереди, времени пребывания в системе, числа заявок в: очереди и в системе.

При среднем времени обслуживания заявки i -ro типа, равном 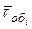, и интенсивности потока заявок этого типа 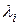Х_г загрузка процессора i-м типом заявок равна 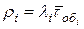. Тогда общая загрузка процессора потоками заявок всех типов будет равна

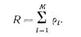
Условие существования стационарного режима в рассматриваемой СМО состоит в выполнении неравенства R<1,0.

Получим выражение для среднего времени ожидания заявок в очереди. Допустим, что в произвольный момент времени в очереди уже находятся l ₁,..., l_М заявок типа 1, 2,.... М и поступила заявка z_i типа i. Тогда время ожидания заявки z_i складывается из следующих компонент:

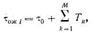
где 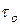— время, необходимое для завершения обслуживания заявки, уже находящейся на обслуживании, T_k — суммарное время обслуживания заявок k -го типа, также уже находящихся в очереди.

Выполняя над левой и правой частями операцию математического ожидания, получаем

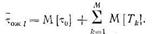
Найдем выражение для М [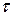₀]. В системе М\G\ 1 среднее время дообслуживания заявки равно:

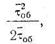
а среднее время ожидания вновь пришедшей заявкой завершения обслуживания равно:

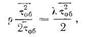
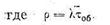
Отсюда следует, что среднее время ожидания заявкой z_i дообслуживания любой заявки должно быть равно взвешенной сумме средних времен дообслуживания:

Среднее время обслуживания заявок k -ro типа, находящихся в очереди, равно:

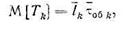
где 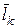—средняя длина очереди заявок k -ro типа. Здесь, используя соотношение

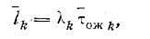
получаем

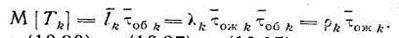
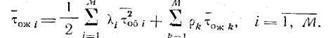
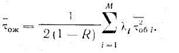
Таким образом, в рассматриваемой системе с бесприоритетной дисциплиной обслуживания среднее время ожидания для заявок всех типов одинаково.

Рассмотрим еще одну характеристику, а именно, среднее-суммарное время обслуживания всех заявок, находящихся в некоторый момент в очереди на обслуживание. В случае многомерного потока имеем:

В теории массового обслуживания показывается, что величина 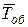не зависит от дисциплины обслуживания и является функцией лишь характеристик СМО. Величина 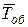находится весьма просто, если рассмотреть СМО с бесприоритетной дисциплиной обслуживания:

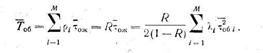
Таким образом, получаем, что для любой дисциплины обслуживания

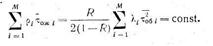
Данное соотношение в теории CMO носит название зако­на сохранения суммарного времени ожидания (заявок в очереди).

3. Характеристики дисциплин обслуживания.

Рассмотрим характеристики дисциплин обслуживания заявок с относительными, абсолютными и смешанными приоритетами применительно к одиночному режиму обслуживания.

Схема организации обработки заявок с относительными приоритетами приведена на рис. 3. Пусть на вход системы обработки поступает поток из Р типов заявок с интенснвностями 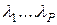, Заявкам типа z_p присвоены приори­теты 1, 2,..., Р в порядке убывания, т. е. большему приоритету соответствует меньшее значение р. Заявка z_p, поступившая в систему, становится в очередь О_р заявок типа z_p. Таким образом, для каждого типа заявок существует своя очередь, где заявки размещаются в порядке поступления. После завершения процессором обслуживания очередной заявки управление передается программе-диспетчеру, которая выбирает первую заявку из очереди с наибольшим приоритетом. Выбранная заявка захватывает процессор на все время обслуживания.

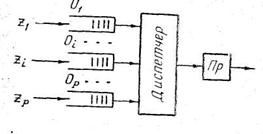
Рис. 3.

Примерный вид зависимости времени обслуживания для дисциплины с относительными приоритетами (ДОП) приведен на рис. 4. Здесь же показано, что для дисциплины обслуживания без приоритетов (ДБП) время обслуживания одинаково для заявок всех типов.

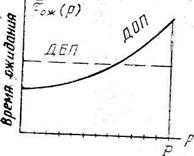
Рис. 4.

Однако в соответствии с законом сохранения времени ожидания суммарное время ожидания для обоих дисциплин одинаково.

Диаграмма характеристик дисциплины обслуживания с относительными приоритетами представлена на рис. 5.

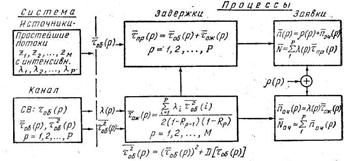
Рис. 5.

Зависимость времени ожидания заявок от их приоритетов при дисциплине обслуживания с абсолютными приоритетами представлена на рис. 6

Смешанная дисциплина обслуживания с матрицей приоритетов называется дисциплиной с тремя классами приоритетов.

Дисциплина ДСП применяется тогда, когда требуется выполнить жесткие ограничения на время ожидания высокоприоритетных типов заявок, и в то же время исключить возможность слишком больших задержек в обслуживании низкоприо­ритетных заявок.

Эффект от введения дисциплины ДСП иллюстрируется рис. 7, где приведена зависимость времени ожидания от приоритета для ДСП с тремя классами приоритетов. На этом рисунке пунктиром показан характер аналогичных зависимостей для дисциплин ДБП, ДОП и ДАП.

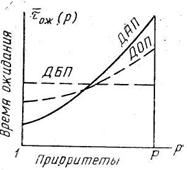
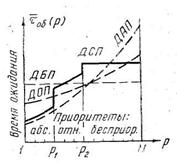
Рис. 6. Рис. 7.

Видно, что дисциплина ДСП обеспечивает такое же качество обслуживания высокоприоритетных заявок, что и дисциплина ДАП, и одновременно время ожидания низкопри­оритетных заявок несколько меньше, чем для дисциплины ДАИ или ДОП и заявки этой группы имеют преимуществ друг перед другом.

Контрольные вопросы:

1. Назовите свойства канала обслуживания?
2. Назовите характеристики процесса обслуживания?
3. Назовите характеристики дисциплины обслуживания?

ЛИТЕРАТУРА

а) основная

1. Барышева, В.К. Теория вероятностей: Учебное пособие / В.К. Барышева, Ю.И. Галанов, Е.Т. Ивлев, Е.Г. Пахомова.- Томск: Изд-во ТПУ, 2009. - 131 с. [Электронный ресурс] //– Режим доступа: http://window.edu.ru/window_catalog/files/r74676/Teor_ver.pdf

б) дополнительная

1. Положинцев, Б.И. Теория вероятностей и математическая статистика: Учебное пособие / Б.И. Положинцев.- СПб.: Изд-во Политехн. ун-та, 2010. - 95 с. [Электронный ресурс] //– Режим доступа: http://window.edu.ru/window_catalog/files/r75165/PBI.pdf

Периодическая литература

1. Информационно-измерительные системы. Радиотехника. Изд. Стандартов.

Internet-ресурсы

1.	http://ibooks.ru/	Электронно-библиотечная система ibooks.ru (Айбукс-ру)
2.	http://www.knigafund.ru/	Электронно-библиотечная система "КнигаФонд"
3.	http://www.gelios-arv.ru	Издательство "Гелиос АРВ"
4.	www.jurnalik.ru	бесплатные русскоязычные журналы
5.	http://www. bnti.ru.	Бюро научно-технической информации
6.	www.osp.ru	Журнал «Открытые системы»

Дата добавления: 2014-01-05