Связь преобразований Фурье и Лапласа

Формула (1.3.7) прямого преобразования Лапласа может рассматриваться как результат определенным образом построенного обобщения одностороннего пре­образования Фурье. Пусть, например, функция удовлетворяет условиям Дирихле в интервале 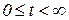, причем при .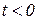

Преобразование Фурье может быть применено к функциям , для которых интеграл существует (условие абсолютной интегрируемости). Этому условию не удовлетворяют многие функции, используемые при анализе про­цессов в автоматических системах, например функции 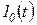; ; 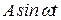; 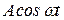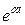(при действительном ); t и др. Для того чтобы иметь возможность подобную функцию преобразовать по Фурье, предварительно её надо умножить на множитель , где вещест­венное число выбрано таким образом, чтобы интеграл

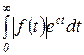
был сходящимся. Значение для каждой функции является вполне определенным. Используя формулу прямого одностороннего преобразования Фурье

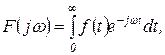
будем преобразовывать по Фурье не функцию , а функцию 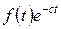, удовлетворяющую условиям применения этого преобразо­вания:

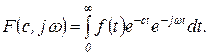(1.3.13)

Введя новую комплексную переменную 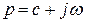, получим:

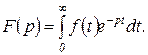
Это выражение представляет собой формулу (1.3.7) прямого преобра­зования Лапласа.

Таким образом, преобразование Лапласа является результатом распространения преобразования Фурье на функции, которые, удов­летворяя условиям Дирихле в интервале 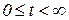, не удовлетво­ряют в этом интервале условию абсолютной интегрируемости.

Рассмотрим теперь формулу обратного преобразования Фурье

Заменив в левой и правой частях этого равенства на 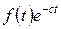, получим

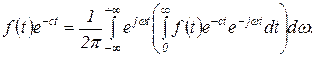
Учитывая, что 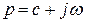, , 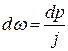найдем

Это равенство, как видно из (1.3.10), является формулой обратного преоб­разования Лапласа.

Таким образом, обратное преобразование Лапласа может рас­сматри­ваться как развитие обратного преобразования Фурье.

Дата добавления: 2014-01-05