Диаграммы Эйлера-Венна

Операции над множествами

Булеан

Мощность множества

Количество элементов n счетного множества A называется мощностью множества и обозначается через n =| A |. Например:

– мощность множества дней недели равна 7;

– мощность множества месяцев года равна 12;

– |{a, b, c}| = 3;

– |{abc}| = 1;

– |{ x | x – целое, x >0, x <100}| = 99.

Множество всех возможных подмножеств некоторого множества A называет множеством-степенью или булеаном множества A и обозначают B (A). Пусть А ={1,2,3}, тогда

B (А)={Æ, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1, 2, 3}}.

Для конечных множеств справедливо следующее утверждение: если A состоит из n элементов, то B (A) состоит из 2 ⁿ элементов, то есть | B (A)|=2^{| A |}. В рассмотренном примере n =| A |=3, поэтому булеан содержит 2³=8 множеств, включая пустое подмножество, и подмножество, равное множеству A. По этой причине булеан иногда обозначают через 2 ^A.

Лекция 2

Итак, нам известны несколько способов задания множеств: перечислением, с помощью характеристического предиката и порождающей процедуры. Еще один способ формирования множества – это выполнение специальных операций над другими множествами. Основными операциями являются:

– объединение множеств;

– пересечение множеств;

– разность множеств;

– дополнение множества;

– симметрическая разность.

Для графической иллюстрации операций над множествами будем использовать так называемые круги Эйлера или диаграммы Венна, называемые в математике диаграммами Эйлера-Венна.

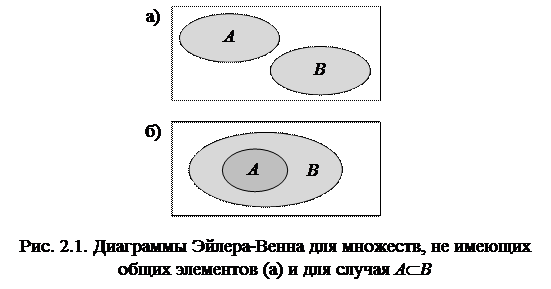
Диаграммы Эйлера-Венна – геометрическое представление множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих рассматриваемые нами множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

На рис. 2.1,а показаны примеры диаграмм Эйлера-Венна для случаев, когда множества A и B не имеют общих элементов (а) и когда A Ì B (б).

Дата добавления: 2014-01-06