Решение задачи синтеза

Решение задачи синтеза основано на формировании внутри регулятора упрежденного вектора состояния . модифицированного объекта управления. Формирование вектора осуществляется с помощью модели объекта, входящей в структуру оптимального регулятора.

Таким образом, оптимальный закон управления должен иметь вид

. (4.10)

или в раскрытом виде

. (4.11)

Такой подход позволяет вычислить компоненты вектора обратных связей регулятора для объекта без учета запаздывания.

Задача определения оптимального управляющего сигнала распадается на две подзадачи:

1). Задача вычисления вектора для системы без запаздывания.

2). Задача формирования упрежденного сигнала .

4.4. Вычисление вектора

Вычисление вектора осуществляется через элементы матицы Риккати

, (4.12)

где матрица Р является единственным положительно определенным решением нелинейного матричного уравнения Риккати

. (4.13)

Раскрывая уравнение Риккати, получим

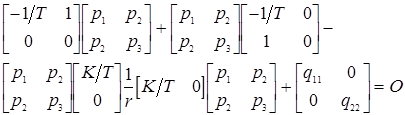
Для упрощения записей введем обозначения , .

Произведя перемножения матриц, получим

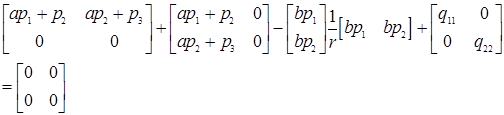Это матричное уравнение распадается на систему алгебраических уравнений вида

;

;

;

.

Из четвертого уравнения вычисляем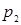

; . (4.14)

Из первого уравнения путем решения квадратного уравнения находим

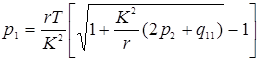. (4.15)

Из второго уравнения вычисляем

. (4.16)

Раскрыв выражения для (подставляя в него ) получим

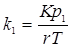; . (4.17)

Знание матрицы Риккати P позволяет наряду с получением коэффициентов вектора , также вычислить численное значение минимальной величины интегрального квадратичного критерия качества

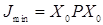. (4.18)

4.5. Нахождение выражения для

Известно, что для объекта без запаздывания уравнение описывающее движение компонент его вектора состояния имеет вид:

. (4.19)

Первая часть выражения является свободной составляющей, которая зависит от динамических свойств объекта управления (матрицы A) и от вектора начальных условий , который характеризует величину начального отклонения системы от положения равновесия.

Интеграл является вынужденной составляющей, определяемой как динамическими свойствами объекта (матрицы A и B), так и видом управляющего сигнала U(S) .

При учете запаздывания в канале управления в уравнении (4.19) вместо сигнала U(S) должен использоваться запаздывающий сигнал . Тогда уравнение (4.19) примет вид

. (4.20)

Из выражения (4.20) получим упрежденный сигнал вектора состояния

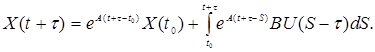
Выделим , и разобьем интеграл на две части

Вынесем за скобки

Заменив выражение в квадратных скобках на X(t) получим формулу для упрежденного вектора состояния

. (4.21)

Сделав замену переменной в выражении (4.21)

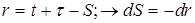, (4.22)

окончательно получим

. (4.23)

Дата добавления: 2014-01-06