Регрессионный анализ. Регрессионная модель

Он проводится с целью получения по экспериментальным данным регрессионных моделей, представляющих собой экспериментальные факторные модели.

Регрессионный анализ включает:

1. статистический анализ результатов эксперимента;

2. получение оценок искомых коэффициентов регрессии ;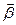

3. оценку адекватности и работоспособности полученной экспериментальной факторной модели.

Под структурой модели понимается вид математических соотношений между факторами 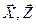и откликом .

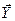Модель в общем виде:

.

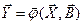Для определения параметров 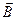используются результаты эксперимента, который представляют в виде функции:

,

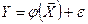где e- аддитивная помеха случайного характера с нормальным законом распределения.

Так как каждый опыт проводится при определенном сочетании уровней факторов 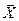, то функцию 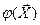представляют:

,

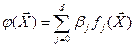где 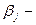j-й элемент вектора искомых коэффициентов уравнения регрессии ;

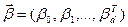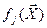- j-я базисная функция – элемент вектора базисных функций .

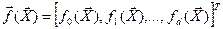В качестве базисных функций используют переменные простейших полиномов, системы ортогональных полиномов (Эрмита, Лежандра, Лаггера) и тригонометрические функции.

Например: полином 1-й степени, описывающий функцию отклика у при двух факторах х₁ и х₂, может иметь вид (линейная регрессия):

;

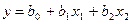или

;

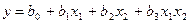а полином 2-й степени (нелинейная регрессия):

.

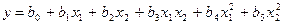Здесь базисные функции:

; ; ; ; ; .

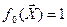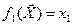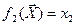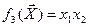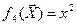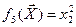Регрессионный анализ применим при следующих предположениях:

1. Аддитивная помеха e – случайная нормально распределенная с параметрам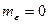и и .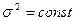

В этом случае функция отклика Y также случайная величина с нормальным законом распределения. Гипотеза о нормальном распределении проверяется по критерию Пирсона;

2. Постоянство дисперсии помехи означает, сто интенсивность ошибки определения Y не меняется при изменении уровня факторов в процессе эксперимента;

3. Значения факторов в активном эксперименте – неслучайные величины, то есть установление фактора на заданном уровне и удерживание его на этом уровне во время опыта точнее, чем ошибка воспроизводимости;

4. Значения помех e в отдельных опытах некоррелированны;

5. Векторы–столбцы базисных функций должны быть линейно зависимыми.

Дата добавления: 2014-01-06