Точки разрыва II рода

1. Ес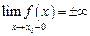ли или 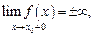то х ₀ – точка разрыва, который называется бесконечный скачок. В этом случае прямая 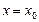является вертикальной асимптотой.

2. Если односторонние пределы в точке х ₀ не существуют (не определены), то х ₀ – точка неопределенности.

Для того чтобы исследовать функцию на непрерывность, необходимо ответить на вопросы:

1) где функция непрерывна;

2) какие точки являются точками разрыва;

3) какой характер разрыва в этих точках?

Пример 1. Пользуясь определением непрерывности доказать, что функция 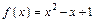непрерывна всюду на R.

Решение. Докажем непрерывность этой функции в произвольной точке .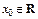

Пусть 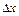– приращение аргумента в точке х ₀. Соответствующее приращение функции имеет вид:

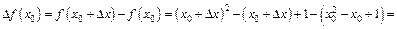
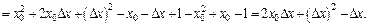
Вычислим предел приращения функции, когда приращение аргумента стремится к нулю:

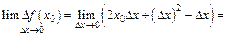
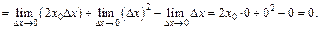
Получили, что 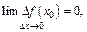что и означает непрерывность функции 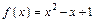на всей числовой прямой, так как х ₀ – произвольная действительная точка.

Пример 2. Найти точки разрыва функции 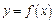и исследовать их характер. Построить схематически график функции в окрестности точек разрыва:

1) 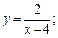2)

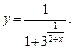
Решение. 1) Функция 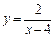определена на всей числовой прямой, кроме х = 4. Данная функция является элементарной, следовательно, она является непрерывной в каждой точке своей области определения. Поэтому единственной точкой разрыва является точка х = 4, в которой функция не определена. Для определения типа разрыва в этой точке вычислим односторонние пределы функции:

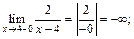
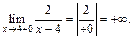
Приходим к выводу, что – точка разрыва II рода (бесконечного скачка).

График функции 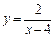в окрестности точки представлен на рис. 16.1.

2) Точкой разрыва данной функции является точка 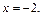Вычислим односторонние пределы заданной функции в точке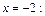

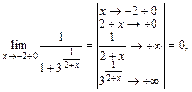
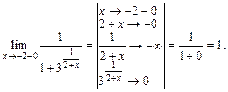
Рис. 16.1

Получили, что оба односторонних предела существуют (и конечны), но не равны между собой. Поэтому – точка разрыва I рода (скачка) – рис. 16.2. Заметим, что скачок равен:

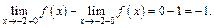
Рис. 16.2

Пример 3. Дана функция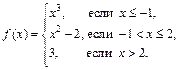

Исследовать ее на непрерывность и разрыв. Построить график.

Решение. На промежутках 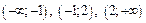заданы аналитические выражения элементарных функций, которые определены и, следовательно, непрерывны на каждом промежутке. Поэтому точками, «подозрительными на разрыв», являются точки 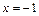и

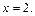
Вычислим односторонние пределы функции в точке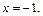

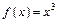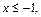Так как функция при то

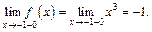
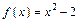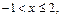Так как функция при то

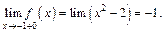
Вычислим значение функции в точке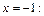

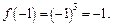
Таким образом, условия непрерывности функции в точке –1 выполнены. Поэтому в точке 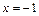разрыва нет.

Вычислим односторонние пределы функции в точке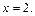

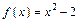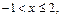Так как функция при то

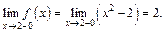
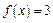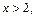Так как функция при то

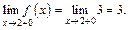
Получили, что 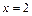– точка разрыва I рода (скачка). Значит, функция непрерывна всюду на числовой прямой кроме точки 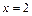(рис. 16.3), в которой она имеет скачок, равный 1.

Рис. 16.3

Пример 4. Дана функция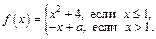

Определить, при каком значении параметра а функция является непрерывной.

Решение. Данная функция определена на всей числовой прямой. Область определения разбивается точкой 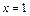на два промежутка: 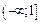и 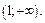На каждом из них задана элементарная функция 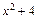и 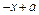соответственно. Для непрерывности заданной функции f (x) на 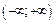необходимо наличие непрерывности в точке 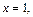т. е. должно выполняться равенство

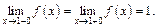
Вычислим односторонние пределы функции в точке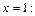

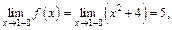
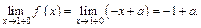
Найдем значение функции в точке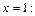

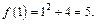
Следовательно, должно выполняться равенство 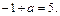Из него получаем 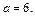При 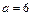функция примет вид:

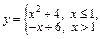
и будет непрерывной на всей числовой прямой.

Пример 5. Используя свойства непрерывных функций, доказать, что уравнение 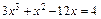имеет хотя бы один корень в промежутке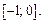

Решение. Рассмотрим функцию 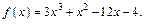Она непрерывна на отрезке 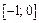как сумма элементарных функций. Вычислим значения функции на концах отрезка:

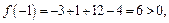
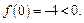
Получаем, что функция на концах отрезка принимает значения разных знаков, потому существует точка 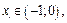в которой функция обращается в нуль, т. е.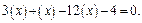

Другими словами, точка х будет являться корнем уравнения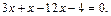

Пример 6. Решить неравенство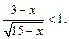

Решение. Решим это неравенство, используя свойства непрерывных функций. Заданное неравенство равносильно следующему:

Функция 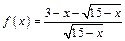определена и непрерывна на промежутке 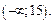Найдем точку, в которой эта функция обращается в нуль. Для этого решим уравнение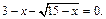

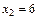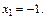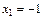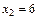Получим два решения и В точках и функция определена, непрерывна и выполняется равенство 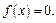Поэтому на каждом из промежутков 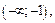(1; 6), (6; 15) функция сохраняет свой знак. Чтобы определить этот знак, достаточно вычислить значение функции в какой-либо одной точке для каждого промежутка.

Пусть 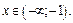На этой полуоси выберем точку 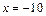и вычислим значение функции:

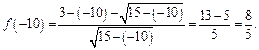
Полученное значение положительно и не удовлетворяет условию (по условию: меньше нуля).

Пусть 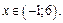Вычислим f (0):

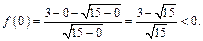
Следовательно, на промежутке (– 1; 6) функция принимает отрицательные значения. Пусть теперь 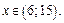Выберем 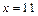и вычисляем:

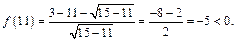
На промежутке (6; 15) функция также отрицательна. Поэтому решением данного неравенства является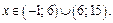

Задания

Дата добавления: 2014-01-06