Элементы комбинаторики

Классическое определение вероятности

Статистическое определение вероятности

Опр. А обозначается (символом Р(А)).

Р(А)=Р*(А) = 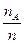(1)

Вероятности Р(А) приписываются свойства:

1.

0 £ Р(А) £ 1.

2.

Р(Æ) = 0.

3.

Р(Ώ) = 1.

4. если А • В = Æ, то

Р(А + В) = Р(А) + Р(В).

т. е. случай w влечет событие A: w Í А.

Опр. А m n

Р(А) =, (2)

Наряду с обозначением Р(А) для вероятности события А используется обозначение р, т. е. р = Р(А).

Из классического определения вероятности вытекают следу­ющие свойства:

1.

0 £ Р(А) £ 1.

2.

Р(Æ) =0.

3.

Р(Ώ) = 1.

4. если А В = Æ, то

Р(А + В) = Р(А) + Р(В).

Пример 4. В урне (емкости) находятся 12 белых и 8 черных шаров. Какова вероятность того, что наудачу вынутый шар будет белым?

Пусть А — событие, состоящее в том, что вынут белый шар. Яс­но, что п = 12 + 8 = 20 — число всех равновозможных случаев (исхо­дов опыта). Число случаев, благоприятствующих событию А, равно 12, т.е. т = 12. Следовательно, по формуле классического определения (2) вероятности имеем: Р(А) =, т.е. Р(А)= 0,6.

Правило умножения (основной принцип): (элемент х) n1 (элемент у) n2, (х и у) п1 • n2.

Пример 5. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если: а) цифры не повторяются? б) цифры могут повторяться

Имеется 5 различных способов выбора цифры для первого места (слева в трехзначном числе). После того как первое место занято, например, цифрой 2, осталось четыре цифры для заполнения второго места. Для заполнения третьего места остается выбор из трех цифр. Следовательно, согласно правилу умножения имеется 5 • 4 • 3 = 60 способов расстановки цифр, т. е. искомое число трехзначных чисел есть 60. (Вот некоторые из этих чисел: 243, 541, 514, 132,...) Понятно, если цифры могут повторяться, то трехзначных чисел 5 • 5 • 5 = (Вот некоторые из них: 255, 333, 414, 111,...)

Правило суммы. х n1, у n2, (х или у), n1 + n2.

Пример 6. В студенческой группе 14 девушек и 6 юношей. Сколь­кими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?

По правилу умножения двух девушек можно выбрать 14 • 13 = 182 способами, а двух юношей — 6 • 5 = 30 способами. Следует выбрать двух студентов одного пола: двух студенток или двух юношей. Соглас­но правилу сложения таких способов выбора будет 182+ 30 = 212.

m (0< m £ n)

Схема выбора без возвращений

n

Размещением n m (0 < m £ n).

(«А из эн по эм»)

= n(n-1)(n-2)... (n-m + 1) (3)

или

= , где n! = l×2×3×..×n 1! = 1, 0! = 1. (4)

Пример 7. Составить различные размещения по 2 из элементов мно­жества D = {а,b,с}; подсчитать их число.

(а, b), (b, а), (а, с), (с, а), (b, с), (с, b) = = 3 • 2 = 6.

Перестановкой n.

Р_п («пэ из эн»)

Р_n = n! (5)

Пример 8. Составить различные перестановки из элементов мно­жества Е = {2,7,8}; подсчитать их число.

(2,7,8); (2,8,7); (7,2,8); (7,8,2); (8,2,7); (8,7,2).

= 3! = 1 • 2 • 3 = 6.

Сочетанием n m (0 £ m £ n).

п.

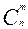(«цэ из эн по эм»)

(6)

или

(7)

Пример 9. Составить различные сочетания по 2 из элементов множества D = {а, b, с}; подсчитать их число.

(а, b); (а,с); (b, с). Их число: = 3

Схема выбора с возвращением

m n размещения с повторениями.

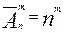(8)

Пример 10. Из 3 элементов а, b, с составить все размещения по два элемента с повторениями.

= 9. Это: (а,а), (а,b), (а,с), (b,b), (b,а), (b,с), (с,с), (с,а), (с, b).

m n сочетания с повторениями.

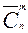
(9)

Пример 11. Из трех элементов а, b, с составить все сочетания по два элемента с повторениями.

=6. (а,а), (а,b), (а, с), (b, b), (b,с), (с, с).

п к 1-й - n₁ раз, 2-й элемент — п₂ раза,..., k -й элемент — п_к раз, причем n₁ + п₂ + … + п_к = n.

n пере­становками с повторениями.

Р_n(n₁, n₂, … n_к)

(10)

Пример 12. Сколько различных пятизначных чисел можно составить из цифр 3, 3, 5, 5, 8?

Здесь п = 5, n₁ = 2, п₂ = 2, n₃ =1. Чи­сло различных пятизначных чисел, содержащих цифры3, 5 и 8, равно Р₅(2,2,1) = =30.

Дата добавления: 2014-01-06