Формула Бернулли. Независимые испытания. Схема Бернулли

Независимые испытания. Схема Бернулли

n А Р(А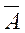) = р

Р( 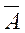) = q = 1 — р

п А т раз (0 £ т £ n).

Обозначается искомая вероятность так: P_n(m) или P_n,_m или Р(m_п = m), где m_п — число появления события А в серии из п опытов.

Например, при бросании игральной кости 3 раза Р₃(2) означает вероятность того, что в 3-х опытах событие А - выпадение цифры 4 — произойдет 2 раза. Очевидно,

Р₃(2) = p²q + p²q + p²q 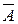= = [(А,А, 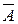);(А, ,А)( 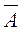,А,А)] =

3p²q =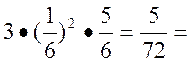0,069.

Теорема 4. п А р, q = 1 — р т формулой Бернулли

P_n(m)=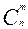×p^m×q^n-m, т=0,1,2,…,n. (29)

Вероятность одного сложного события, состоящего в том, что со­бытие А в п независимых опытах появится т раз в первых т опы­тах и не появится (n — т) раз в остальных опытах (это событие 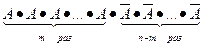) по теореме умножения вероятностей равна p^mq^n-m. Вероятность появления события А снова т раз, но в другом порядке (например, 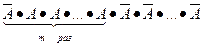или А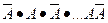 и т. д.)

будет той же самой, т. е. p^mq^n-m.

Число таких сложных событий — в п опытах т раз встречается со­бытие А в различном порядке — равно числу сочетаний из п по m, т. е. 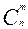. Так как все эти сложные события несовместны, то по теореме сло­жения вероятностей искомая вероятность равна сумме вероятностей всех возможных сложных событий, т. е.

P_n(m)= 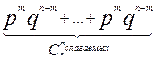=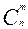×p^m×q^n-m, m =0, l,...,n.

Можно заметить, что вероятности Р_п(т), m = 0,1,..., n являются коэффициентами при х^m в разложении (q + рx)ⁿ по формуле бинома Ньютона:

(q+рх)^п = qⁿ + 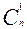q^n-1 px + 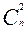q^n-2 p² x² +... + 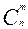×q^n-m p^m x^m+... + pⁿxⁿ.

Поэтому совокупность вероятностей Р_п(т) называют биномиальным законом распределения вероятностей (см. п. 2.7), а функцию j(x) = (q + рх)^п — производящей функцией для последовательности неза­висимых опытов.

Если в каждом из независимых испытаний вероятности наступле­ния события A разные, то вероятность того, что событие А наступит т раз в п опытах, равна коэффициенту при m-й степени многочлена j_n(z) = (q₁ + p₁x)(q₂ + p₂x ) •... • (q_n + p_nx ), где j_n(z) - производящая функция.

п k событий А₁, А₂, …,А_k

p₁, p₂,..., p_k,

событие А₁ появится m₁ раз,

событие А₂— m₂ раз,

...,

событие А_k — m_k раз,

равна P_n(m₁,m₂,...,m_k)=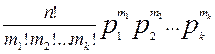 (30), где m₁+m₂+...+m_k=n.

Пример 21. Производится 3 независимых выстрела по цели. Веро­ятности попадания при разных выстрелах одинаковы и равны р = 0,9. Какова вероятность: а) промаха; б) одного попадания; в) двух попаданий; г) трех попаданий?

В данном случае n = 3, р = 0,9, q = 0,1. Пользуясь формулой Бернулли (29), находим:

а) Р₃(0) = 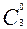• 0,9⁰ • 0,1³ = 0,001 — вероятность трех промахов;

б) Р₃(1) = 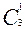• 0,9¹ • 0,1² = 3 • 0,9 • 0,01 = 0.027 — вероятность одного попадания;

в) Р₃(2) = • 0,9² • 0,1¹ = 3 • 0,81 • 0,1 = 0,243 — вероятность двух попаданий;

г) Р₃(3) = 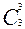• 0,9³ • 0,1⁰ = 0,9³ = 0,729 — вероятность трех попаданий.

Эти результаты можно изобразить графически, отложив на оси Ох- значения m, на оси Оy — значения 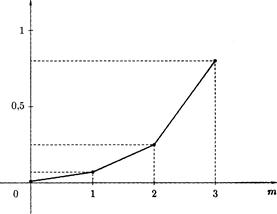Р_n(m)

Р_n(m)

Рис. 14

Ломаная, соединяющая точки (0; 0,001), (1; 0,027), (2; 0,243), (3; 0,729), называется многоугольником распределения вероятностей.

Если вероятности при разных выстрелах различны, то производящая функция имеет вид j₃ (z) = (0,3 + 0,7z)(0,2 + 0,8z)(0,l + 0,9z) = 0,504z³ + 0,398z² + 0,092z + 0,006. Откуда находим вероятность трех, двух, одного попаданий, промаха соответственно: Р₃(3) = 0,504, Р₃(2) = 0,398, Р₃(1) = 0,092, Р₃(0) = 0,006. (Контроль: 0,504 + 0,398 + 0,092 + 0,006 = 1.)

Глава 2.Случайные величины

Дата добавления: 2014-01-06