Закон распределения дискретной случайной величины. Многоугольник распределения

Понятие случайной величины. Закон распределения случайной величины

Случайные величины (сокращенно: с. в.) обозначаются прописны­ми латинскими буквами Х,У, Z,... (или строчными греческими буква­ми ξ (кси), η(эта), θ (тэта), ψ (пси) и т. д.), а принимаемые ими значения соответственно малыми буквами х₁, х₂ ,…, у₁, у₂, у₃ …

Примерами с. в. могут служить: 1) X — число очков, появляющих­ся при бросании игральной кости; 2) У — число выстрелов до первого попадания в цель; 3) Z — время безотказной работы прибора и т. п. (рост человека, курс доллара, количество бракованных деталей в пар­тии, температура воздуха, выигрыш игрока, координата точки при слу­чайном выборе ее на [0; 1], прибыль фирмы,...).

Случайной величиной X Ώ w

X(w), т.е. X = X(w), w Î Ώ (или X = f (w)) (31)

Пример1. Опыт состоит в бросании монеты 2 раза. На ПЭС Ώ={ w₁, w₂, w₃, w₄}, где w₁ = ГГ, w₂ = ГР, w₃ = РГ, w₄ = РР, можно рассмотреть с. в. X — число появлений герба. С. в. X является функ­цией от элементарного события w_i: X( w₁ ) = 2, X( w₂ ) = 1, X( w₃ ) = 1, X( w₄ )= 0; X — д. с. в. со значениями x₁ = 0, x₂ =1, x₃ = 2.

X(w) S Р(А) = Р(Х < х).

X — д. с. в.,

x₁, x₂, x₃,…,x_n,…

p_i, где i = 1,2,3,...,n,….

Закон распределения д. с. в. p_i=Р{Х=x_i }, i=1,2,3,...,n,...,

с. в. X x _i.:

X	x1	x2	….	xn	…
P	p1	p2	….	pn	…

Так как события {X = x₁}, {X = x₂},…, {X = x_n}, т.е. .

(x₁, p₁ ), (x₂, p₂),…, (x_n, p_n) называют многоугольником (или полигоном) рас­пределения (см. рис. 17).

Рис. 17

Случайная величина X дискретна, если существует конечное или счетное множество чисел x₁, x₂,..., x_n таких, что Р{Х = x_i} = p_i > 0 (i = 1,2,...) p₁ + p₂ + p₃ +…= 1 (32)

Суммой д. с. в. X, принимающей зна­чения x_i с вероятностями p_i = Р{Х = x_i }, i = 1,2,3,...,n, и д. с. в. Y, при­нимающей значения y_j с вероятностями p_i = Р{Y = y_j }, j = 1,2,3,...,m, называется д. с. в. Z = X + Y, принимающая значения z_ij = x_i + y_j с вероятностями p_ij = Р{ Х = x_i,Y = y_j }, для всех указанных значений i и j. В случае совпадения некоторых сумм x_i + y_j соответствующие вероятности складываются.

Разностью д. с. в. X, принимающей зна­чения x_i с вероятностями p_i = Р{Х = x_i }, i = 1,2,3,...,n, и д. с. в. Y, при­нимающей значения y_j с вероятностями p_i = Р{Y = y_j }, j = 1,2,3,...,m, называется д. с. в. Z = X — Y, принимающая значения z_ij= x_i – y_j с вероятностями p_ij = Р{ Х = x_i,Y = y_j }, для всех указанных значений i и j. В случае совпадения некоторых разностей x_i – y_jсоответствующие вероятности складываются.

Произведением д. с. в. X, принимающей зна­чения x_i с вероятностями p_i = Р{Х = x_i }, i = 1,2,3,...,n, и д. с. в. Y, при­нимающей значения y_j с вероятностями p_i = Р{Y = y_j }, j = 1,2,3,...,m, называется д. с. в. Z = X × Y, принимающая значения z_ij = x_i × y_j с вероятностями p_ij = Р{ Х = x_i,Y = y_j }, для всех указанных значений i и j. В случае совпадения некоторых произведений x_i × y_jсоответствующие вероятности складываются.

д. с. в. сХ, с x_i р_i = Р{Х = x_i }.

X и Y события {X = x_i } = А_i и {Y = y_j } = В_j независимы для любых i= 1,2,...,n; j = l,2,...,m, т.е.

P{X = x_i;Y = y_j } =P{X = x_i } ×P {Y = y_j } (33)

Пример 2. В урне 8 шаров, из которых 5 белых, остальные — чер­ные. Из нее вынимают наудачу 3 шара. Найти закон распределения числа белых шаров в выборке.

Возможные значения с. в. X — числа белых шаров в выборке есть x₁= 0, x₂ = 1, x₃ = 2, x₄= 3. Вероятности их соответственно будут р₁ = Р{Х = 0} = , р₂ = Р{Х = 1} = , р₃ = Р{Х = 2} = , р₄ = Р{Х = 3} = , Закон распределения запишем в виде таблицы.

X
Р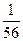

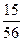
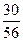
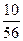
(Контроль: 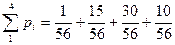=1)

Дата добавления: 2014-01-06