
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Х и м и ч е с к о е р а в н о в е с и е
|
|
|
|
Зависимость ЭДС от температуры
В случае самопроизвольного процесса: 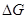 < 0, Emax > 0. Из (2.17):
< 0, Emax > 0. Из (2.17):
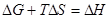 ,
,
где 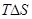 – теплота при обратимом процессе,
– теплота при обратимом процессе, 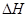 – теплота, когда не совершается полезная работа.
– теплота, когда не совершается полезная работа.
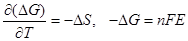
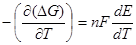
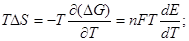
 , где
, где 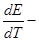 температурный коэффициент.
температурный коэффициент.
Тепловой эффект гальванического элемента: 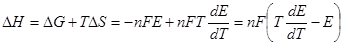 (3.10)
(3.10)
Общее условия химического равновесия.
Изобарный потенциал гомогенной многокомпонентной системы представляет собой однородную функцию первого порядка по числу молей компонентов:
G = G (T,p,n1,n2,…). (4.1)
GT,p= 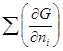 T,p,n
T,p,n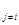 dni =
dni =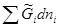 =
=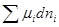 ,
,
где 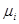 =
=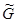 =
=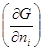 T,p,n
T,p,n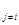 - (4.2)
- (4.2)
Химический потенциал i-го компонента равен приращению изобарного потенциала при добавлении одного моля этого компонента к большому объему системы при постоянных температуре и давлении и постоянных количествах других компонентов.
Рассмотрим находящуюся в неизменных внешних условиях термодинамическую систему, в которой самопроизвольно протекает химическая реакция:
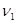
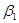 +
+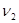
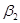 + …=
+ …= 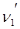
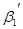 +
+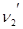
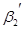 + … (4.3)
+ … (4.3)
Сразу после контакта исходных веществ в системе образуются продукты прямой реакции, которые, в свою очередь, вступают в химическое взаимодействие с образованием исходных веществ (обратная реакция). По мере протекания самопроизвольного процесса число молекул исходных веществ, реагирующих в единицу времени (скорость прямой реакции) снижается, так как концентрации исходных веществ уменьшаются, а скорость обратной реакции увеличивается. Когда скорости прямой и обратной реакции сравняются, наступает состояние химического равновесия, характеризуемое постоянством числа молекул исходных и конечных веществ. В состоянии химического равновесия число молекул исходных веществ, вступающих в единицу времени в прямую реакцию, равно числу молекул конечных веществ, участвующих в обратном процессе за тот же промежуток времени.
С изменением внешних условий химическое равновесие нарушается, что вызывает изменение концентраций реагирующих веществ и всех термодинамических функций, характеризующих состояние системы. С течением времени система вновь придет в состояние равновесия, которое будет характеризоваться минимальным в данных условиях значением соответствующего термодинамического потенциала.
Чаще всего химические реакции протекают в условиях постоянства давления и температуры. В этом случае при достижении равновесия изобарно-изотермический потенциал принимает минимальное значение:
dG = 0 (4.4)
Полный дифференциал изобарно-изотермического потенциала гомогенной многокомпонентной системы имеет вид
dG = - SdT + Vdp +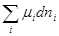 (4.5)
(4.5)
Учитывая, что все вещества системы участвуют в химической реакции, изменение числа молей можно представить как
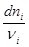 =
=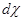 , (4.6)
, (4.6)
где 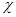 – химическая переменная.
– химическая переменная.
Тогда уравнение (4.5) принимает форму:
dG = - SdT + Vdp + 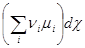 (4.7)
(4.7)
Из выражения (4.7) следует, что при протекании в системе одной химической реакции, изобарно-изотермический потенциал является функцией трех переменных:
G = G (T,p,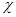 ) (4.8)
) (4.8)
и, следовательно,
dG = 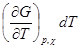 +
+ 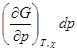 +
+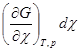 (4.9)
(4.9)
Из уравнения (4.7) и (4.9) следует, что
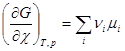 (4.10)
(4.10)
Так как химическая реакция протекает при условии постоянства давления и температуры, то
dG = 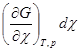 =
=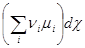 (4.11)
(4.11)
В состоянии химического равновесия выполняется уравнение (4.4) и из (4.11) следует, что
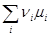 = 0 и
= 0 и 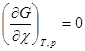 (4.12)
(4.12)
Уравнения (4.11) и (4.12) выражают в общем виде условие химического равновесия.
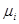 (р) =
(р) =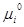 + RT lnрί (4.13)
+ RT lnрί (4.13)
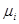 (с) =
(с) =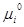 + RT lnсί (4.14)
+ RT lnсί (4.14)
Для реальных газов уравнения (4.13) и (4.14). являются лишь некоторым приближением, работающим при низких давлениях. Для сохранения формы уравнения давление (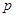 ) заменяют другой величиной – летучестью или фугитивностью (f). Летучестью называется такое давление реального газа, при котором газ ведет себя как идеальный (величина имеет размерность давления):
) заменяют другой величиной – летучестью или фугитивностью (f). Летучестью называется такое давление реального газа, при котором газ ведет себя как идеальный (величина имеет размерность давления):
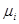 (f) =
(f) =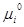 + RT ln fί (4.15)
+ RT ln fί (4.15)
Чтобы найти летучесть, обычно ее выражают через p
f = 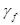
 p, где
p, где 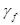 – безразмерная величина, называемая коэффициентом летучести. (
– безразмерная величина, называемая коэффициентом летучести. (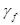 =
= 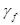 (T, p)).
(T, p)).
Перепишем (4.15):
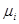 (f) =
(f) = 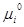 +RT ln
+RT ln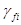 + RT ln pί (4.16)
+ RT ln pί (4.16)
Таким образом, летучесть (фугитивность) – величина, которую надо подставить в выражение для химического потенциала идеального газа, чтобы получить значение химического потенциала реального газа. Аналогично для растворов, где мерой количества вещества является молярная концентрация:
p=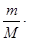 RT
RT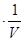 =CRT
=CRT
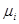 (C2) =
(C2) = 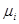 (C1) + RT ln
(C1) + RT ln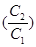 , С1 = 1 моль.
, С1 = 1 моль.
для идеальных: 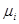 (Сi) =
(Сi) =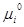 + RT ln Сί
+ RT ln Сί
для реальных: 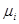 (Сi) =
(Сi) = 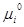 + RTln
+ RTln 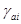 + RT ln αί (4.17)
+ RT ln αί (4.17)
aί – активность компонента ί;
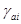 – коэффициент активности компонента ί.
– коэффициент активности компонента ί.
Равновесие в реакциях, протекающих в газовой фазе.
Общее условие равновесия системы можно записать так:
∆G = 0 или ∑ 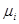 dnί = 0, другими словами
dnί = 0, другими словами
условие равновесия – равенство нулю суммы мольных значений свободной энергии Гиббса (или химических потенциалов).
Для реакции
aA + bB = cC + dD
∆G = ∑∆Gпрод – ∑∆Gисх = (c∆GC + d∆GD – b∆GB – a∆GA), но
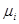 (p) =
(p) =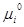 + RT ln pί ,
+ RT ln pί ,
Следовательно, ∆G = c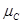 + d
+ d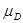 – b
– b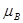 – a
– a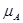 = c
= c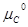 + d
+ d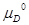 – b
– b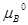 – a
– a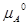 +
+
+ RT(c ln pC + d ln pD – b ln pB – a ln pA) =
= ∆Gо + RT ln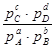 (4.18)
(4.18)
Мы получили изотерму химической реакции или изотерму Вант-Гоффа, где под знаком логарифма ставится константа равновесия (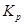 ) для химической реакции между газами.
) для химической реакции между газами.
В условиях равновесия ∆G0 + RT ln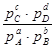 = 0, где
= 0, где 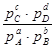 =
= 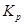 ,
,
ln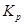 = –
= –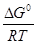 (4.19)
(4.19)
Таким образом, 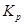 можно рассчитать из величины энергии Гиббса,
можно рассчитать из величины энергии Гиббса, 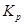 в этом случае выражается в единицах давления в степени ∆n (в атмосферах или Па).
в этом случае выражается в единицах давления в степени ∆n (в атмосферах или Па).
Равновесие в реакциях, протекающих в растворах.
Воспользовавшись (4.18), получим
∆G0 + RT ln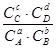 = 0 (4.20),
= 0 (4.20),
откуда 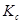 =
= 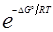 =
= 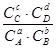 .
.
Или более применимая для термодинамических расчетов реальных растворов константа 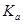 =
= 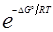 =
= 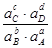
Рассмотрим связь между 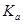 и
и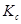 :
:
ai =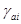
 Ci
Ci
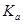 =
= 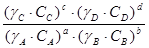 =
=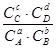

 =
=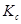

 (4.21)
(4.21)
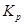 и
и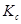 :
:
pV = 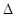 nRT; p =
nRT; p =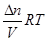 ;
; 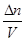 = C (молярная концентрация), следовательно
= C (молярная концентрация), следовательно
p = СRT
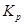 =
=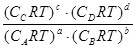 = (RT)c+d-b-a
= (RT)c+d-b-a
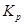 = (RT)
= (RT)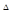 n
n 
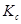
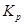 – величина, позволяющая количественно выразить химическое равновесие и условия, определяющие выход продуктов реакции.
– величина, позволяющая количественно выразить химическое равновесие и условия, определяющие выход продуктов реакции.
Равновесие в гетерогенных системах.
Если система находится в состоянии равновесия, то должно выполняться условие равенства всех интенсивных параметров во всех присутствующих фазах. Это справедливо и для химических потенциалов. Таким образом, для реакции
BaSO4 ↔ Ba2+ (раствор) + SO42- (раствор)
Химический потенциал иона Ba2+ (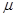 Ba2+) в насыщенном растворе BaSO4 равен
Ba2+) в насыщенном растворе BaSO4 равен 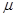 Ba2+ в осадке. Хотя реальное различие в концентрациях может достигать десяти и более порядков.
Ba2+ в осадке. Хотя реальное различие в концентрациях может достигать десяти и более порядков.
Рассмотрим процесс разложения CaCO3.
CaCO3 = CaO + CO2 ↑
CaO и CO2 не образуют твердых растворов. Таким образом, концентрация этих веществ в области протекания реакции равны, а, следовательно, и их химические потенциалы не будут меняться вплоть до полного исчезновения одного из компонентов и будут равны соответствующим стандартным величинам, а для CO2:
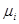 =
= 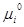 + RT ln
+ RT ln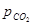 ,
,
отсюда при равновесии при атмосферном давлении:
∆G = 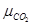 + µCaO –
+ µCaO – 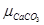 =
= 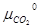 + RT ln
+ RT ln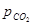 +
+ 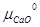 –
– 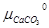 = ∆G0 CaCO3 + RT ln
= ∆G0 CaCO3 + RT ln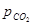 или
или
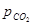 =
=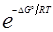
Таким образом, 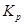 в этом случае является парциальным давлением CO2. В общем случае для получения
в этом случае является парциальным давлением CO2. В общем случае для получения 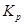 гетерогенного процесса с участием газов следует учитывать лишь парциальное давление газов. Аналогичное заключение и для реакций в растворах, сопровождающихся выпадением или растворением осадка.
гетерогенного процесса с участием газов следует учитывать лишь парциальное давление газов. Аналогичное заключение и для реакций в растворах, сопровождающихся выпадением или растворением осадка.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 315; Нарушение авторских прав?; Мы поможем в написании вашей работы!