Правило Фаз Гиббса

Ф а з о в ы е р а в н о в е с и я.

Предположим, что гетерогенная система состоит из ф фаз, в каждую из которых входят к компонентов. В дальней­шем нижними индексами будем обозначать компоненты системы, а верхними фазы (так как это сделано в выражении (5.1) для обоз­начения химических потенциалов).

При равновесии многокомпонентной гетерогенной системы должны выполняться следующие условия.

а) условие термического равновесия:

T¹ = T² = … = T ^ф (5.2)

б) условие механического равновесия:

p¹ = p² = … = p ^ф (5.3)

в) условие химического равновесия:

= = … =

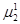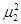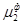= = … = (5.4)

= = … =

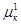Выражения (5.2) и (5.3) представляют собой ряды тождеств, так как температура и давление являются независимыми переменными. Химические потенциалы представляют собой функции, зависящие от температуры, давления и концентраций. Общий вид этих функций может быть выражен, например, таким образом:

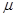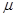= (p, T, x₁, x₂, … x_к) (5.5)

где x₁, x₂, …, x_к - концентрации.

При переходе от одной фазы к другой вид функции (5.5) меняется, поэтому равенства типа

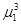= ; = и т.д. представляют собой уравнения.

Каждая cтрока системы (5.4) позволяет составить (ф - 1) независимых уравнений. Число cтрок в системе равно к, поэ­тому общее число независимых уравнений

к (ф - 1) (5.6)

В число независимых переменных входят температура, давле­ние и концентрации компонентов. В каждой фазе к компонентов, но при заданных температуре и давлении выбрать произвольно к концентрации нельзя. Например, для смеси не реагирующих между собой идеальных газов согласно закону Дальтона:

p = p₁ + p₂ + … + p_к

При заданном общем давлении p можно произвольно менять парциальные давления кроме одного. Следовательно, независимых переменных в этой случае (к - 1).

Другой пример: жидкий раствор, в состав которого входят к компонентов с концентрациями x₁, x₂, … x_к, выраженные в мольных долях. Ясно, что x₁ + x₂ + … + x_к = 1, и, следо­вательно, при произвольной изменении (к - 1) концентрации, выбор последней концентрации определится уравнением 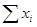= 1.

Для каждой фазы можно записать уравнение состояния, кото­рое связывает температуру, давление и концентрации компонентов, поэтому число независимых концентраций в каждой фазе (к - 1). Общее число независимых переменных с учетом температуры и дав­ления будет:

ф (к - 1) + 2 (5.7)

Если число независимых переменных (5.7) больше числа независимых уравнений (5.6), то разность этих двух чисел

С = ф (к - 1) + 2 - к (ф - 1)

представляет собой число переменных, которым можно придавать произвольные значения при данном числе фаз.

С – число степеней свободы

С = к + 2 - ф (5.8)

Соотношение (5.8) называется законом фазового равновесия или правилом фаз Гиббса.

Число степеней свободы - число независимых переменных (давление, температура, концентрации), которые можно менять в некоторых пределах без изменения числа фаз. Система, имеющая две степени свободы, называется бивариантной, а имеющая одну степень свободы - моновариантной. Если числи степеней свободы равно нулю, то такая система инвариантна.

Фазовое равновесие в однокомпонентных системах.

Уравнение Клапейрона-Клаузиуса

Рассмотрим закономерности, связанные с превращением од­ной фазы чистого вещества в другую: испарение, плавление, пе­реход твердого тела из одной модификации в другую. Для приме­ра возьмем равновесие между жидкостью и её паром при постоян­ных температуре и давлении. Для этого поместим жидкость на дно цилиндра, погруженного в термостат. Давление пара, находящегося в равновесии с жидкостью, уравновешено внешним давлением (Рис.10).

Рис.10

Условие равновесия такой системы согласно (4.12):

В силу постоянства состава в однокомпонентной системе химический потенциал тождественен мольному термодинамическому потенциалу ().

Следовательно, условие равновесия может быть записано так:

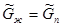. (5.9)

При повышении давления на бесконечно малую величину dp мольные изобарно-изотермические потенциалы жидкости и пара изменяются также на бесконечно малую величину:

dG = - SdT + Vdp

При Т =const для одного моля жидкости и пара соответственно получим:

Так как мольный объем пара () больше мольного объема жидкости (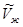), то 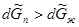при установлении нового состояния равновесия часть пара должна превратиться в жидкость. Этот вы­вод согласуется с принципом Ле Шателье-Брауна, согласно которому под воздействием внешних сил система должна так изменить свое состояние, чтобы уменьшить это воздействие. Если при по­стоянном давлении повысим температуру на dТ, то изменение изобарно-изотермических потенциалов жидкости и пара будет иметь вид:

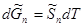
Ясно, что 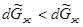,так как мольная энтропия пара () больше мольной энтропии жидкости (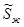). Следовательно, при установлении нового состояния равновесия часть жидкости должна будет испаряться. Это также подтверждается принципом Ле Шателье-Брауна, так как при повышении температуры в системе должны идти процессы с поглощением тепла.

В самом общем случае при постоянных температуре и давлении равновесие двух фаз однокомпонентной системы:

1 фаза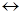2 фаза

можно записать, как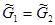

После одновременного изменения температуры на dT и давления на dp установится новое состояние равновесия:

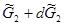
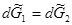
Запишем уравнения полных дифференциалов для изобарно-изотермических потенциалов 1 и 2 фаз:

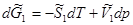
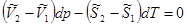
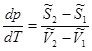(5.10)

Для разновесных изотермических фазовых переходов

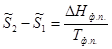
(5.11)

где – мольная теплота фазового перехода,

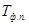– температура фазового перехода.

Подставим (5.11) в уравнение (5.10), получим

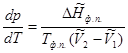(5.12)

Уравнение (5.12) называется уравнением Клапейрона-Клаузиуса.

Фазовые переходы 1 рода.

Фазовые переходы, характеризующиеся равенством изобарно-изотермических потенциалов равновесных фаз и скачкообразным изменением энтропии и объема при переходе вещества из одной фазы в другую, называется фазовыми переходами первого рода.

Энтропия и объем являются первыми производными изобарно-изотермического потенциала по соответствующим переменным (см. раздел Термодинамика):

;

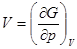
Поэтому фазовые переходы 1 рода характеризуются скачкообраз­ным изменением первых производных изобарного потенциала.

Испарение - пример фазового перехода 1 рода:

Переход жидкой фазы в газообразную сопровождается погло­щением тепла (). Мольный объем газа всегда больше соответствующего объема жидкости 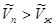Поэтому при фазовом переходе в уравнении Клапейрона-Клаузиуса. (5.12) производная 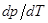всегда положительна. Следовательно, темпе­ратура испарения всегда повышается с ростом давления.

При температурах, далеких от критической, мольной объем пера всегда во много раз превосходит мольный объем жидкости. Поэтому можно пренебречь мольным объемом жидкости в уравнении (5.12), которое принимает вид:

(5.13)

Если пар вдали от критической точки считать идеальным газом, то

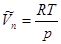(5.14)

Подставим (5.14) в уравнение (5.13) и проинтегрируем получен­ное выражение, считая 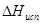постоянной величиной в неболь­шом интервале температур:

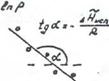
Представив зависимость давления насыщенного пара от температуры в координатах , можно найти мольную теплоту ис­парения (Рис.11).

В действительности теплота испарения в области температур далекой от критической, немного уменьшается с ростом температуры и сильно убывает вблизи критической точки, при которой 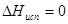.Аналогичным уравнением описывается сублимация твердого тела.

Теплоты испарения различных жидкостей связаны с температурами кипения эмпирическим правилом Трутона: изменение мольной энтропии испарения различных жидкостей при нормальной температуре кипения одинаковы:

(5.15)

Это правило не выполняется для ассоциированных и полярных жидкостей.

Плавление является также примером фазового перехода 1 рода и к нему применимо уравнение Клапейрона-Клаузиуса:

тв. тело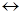жидкость

(I) (П)

Для этого процесса

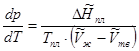(5.16)

Теплота плавления - теплота перехода твердой фазы в жидкую – положительна 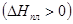. Мольные объемы твердого тела и жидкости сравнимы между собой. Для большинства веществ мольный объем жидкости больше мольного объема твердого тела (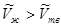). В этом случае из уравнения (5.16) следует, что производная 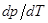положительна, а это значит, что с повышением давления увеличивается температура плавления. Для таких веществ, как вода, висмут и некоторых других при температуре плавления мольный объем жидкости меньше мольного объема твердого тела (). 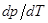Следовательно,< 0 и с повышением давления температура плавления указанных веществ понижается.

Фазовые переходы 2 рода

Фазовые переходы, при которых не изменяются не только изобарно-изотермический потенциал (Δ G = 0 ), но и его первые производные (Δ V = 0, ΔS = 0), а скачкообразно изменяются вторые производные:

(5.17)

называются фазовыми переходами второго рода.

Фазовые переходы второго рода не сопровождаются тепловы­ми эффектами. К фазовым переходам второго рода относятся пе­реходы металла в сверхпроводящее состояние, ферромагнитных ве­ществ в парамагнитные, изменения типа симметрии кристаллов. Как видно из выражений (5.17), о наличии фазовых переходов второго рода можно судить по скачкообразным изменениям на кри­вых, характеризующих температурные зависимости теплоемкости и мольного объема.

Диаграмма состояния воды.

Графическое изображение зависимости состояния системы и фазовых равновесий в ней от внешних условий и от её состава называется диаграммой состояния или фазовой диаграммой.

Рис.12 Диаграмма состояния воды.

На Рис. 12 приведена диаграмма воды в области средних давлений. Область диаграммы левее кривой AОB соответствует твердому состоянию (лёд). Область диаграммы ниже кри­вой АОС соответствует газообразно­му состоянию воды. Часть диаграммы, заключенная между кривыми ОВ и ОС, отвечает жидкому состоянию. Кривые ОА, ОВ, ОС соответствуют равновесию между соответствующими двумя фазами. Кривая ОА выражает зависимость давления насыщен­ного пара надо льдом от температуры. Кривая ОВ изображает зави­симость температуры плавления льда от давления. Наклон кривой OB влево свидетельствует об отрицательной значении производ­ной 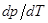, т.е. температура замерзания понижается с повышением давления.

Кривая ОС характеризует зависимость давления насыщенного пара жидкой воды от температуры. Все рассмотренные кривые начинаются в точке О, которая соответствуют сосуществованию трех агрегатных состояний воды: жидкого, твердого и газообразного. Эта точка называется тройной.

Рассчитать число степеней свободы в точке О, можно воспользоваться правилом фаз Гиббса (5.8). Рассматривая система однокомпонентная (к = 1) и в данной точке Ф = 3, так как три фазы находятся в равновесии. С = к + 2 – ф = 1 + 2 – 3 = 0, что означает, что указанному состоянию соответствует строго определенные значения Т и р: 273,16 К и 0,006 атм. Точка а, лежащая на кривой АО, соответствует равновесию двух фаз: льда и пара. Число степеней свободы в этой точке С = 1 + 2 – 2 = 1, что означает, что изменение одного параметра (например температуры) повлечет за собой изменение другого (давления) при сохранении равновесия твердой и газообразной фазы. Уравнение Клапейрона-Клаузиуса (5.12) позволяет рассчи­тать значение давления при заданном изменении температуры.

Число степеней свободы в точке в равно 2, так как в этой точке всего одна фаза:

С = I + 2 – 1 = 2. Это означает, что в определенных интервалах можно менять температуру и дав­ление при сохранении жидкой фазы. Пределы изменения температу­ры и давления определяются кривыми OB и ОС.

Однако при осторожном охлаждении воды можно получить её в переохлажденном состоянии. Пунктирная кривая ОД отвечает давлению насыщенного пара над переохлажденной жидкостью. Такое состояние неустойчиво и носит название метастабильного. Кривая ОД расположена выше кривой ОА, которая характеризует зависи­мость давления насыщенного пара надо льдом. При попадании в со­суд с переохлажденной водой твердых частиц или при легком ударе о сосуд переохлажденная вода переходит в лёд без изменения температуры. Возможность такого самопроизвольного пере­хода вытекает из следующих рассуждений. При постоянной температуре . Считая, что при низких давлениях пар пред­ставляет собой идеальный газ, получим

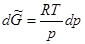
Проинтегрировав последнее выражение, имеем:

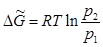
(5.18)

Как видно из Рис. 12, р₂ < р₁, а следовательно в уравнении (5.18) ΔG <О. Таким образом, переход из метастабильного состоя­ния, представляющего собой переохлажденную жидкость с давлением насыщенного пара p₁ (точка ), в устойчивое твердое состояние с давлени­ем пара p₂ (точка а) самопроизвольный.

Равновесие бинарного жидкого раствора, состоящего из летучих веществ,с паром.

Пар, находящийся в равновесии в равновесии с жидкостью, называется насыщенным паром. Жидкости, которые при данной температуре имеют до­статочно высокое давление пара, называются летучими.

В самом общем случае жидкий раствор, представляющий собой смесь летучих жидкостей, находится в равновесии с паром, состоя­щим из тех же компонентов, что и жидкая фаза. Давление насыщенного пара над жидким раствором будет определяться суммой парци­альных давлений компонентов. Однако, когда в состав жидкой фазы входят нелетучие вещества, последние могут отсутствовать в га­зовой фазе.

Рассмотрим раствор двух летучих жидкостей А и В. Мольную долю компонента В обозначим x, тогда мольная доля компонента А будет равна (1-х). При постоянной температуре давление насыщен­ного пара будет функцией только состава раствора. На диаграмме, представленной на рис 13, изображена зависимость давления насыщенного пара раствора от его состава. По оси абсцисс слева направо обычно откладывают мольную долю компонента В, имеющего в чистом виде более высокое давление насыщенного пара и поэтому более низ­кую температуру кипения. Мольную долю компонента А легко вычис­лить, учитывая, что сумма мольных долей обоих компонентов, равны единице.

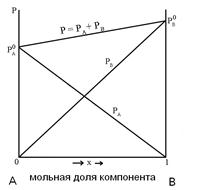
Рис. 13

Из рис.13 видно, что давление насыщенного пара каждого из компо­нентов пропорционально его мольной доле в растворе, а коэффициентом пропорциональности является давле­ние насыщенного пара чистого вещества.

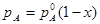(5.19)

(5.20)

Приведенные соотношения, полу­ченные экспериментально, носят наз­вание закона Рауля. Выражение (5.19) легко преобразовать:

(5.21)

Относительное понижение давление пара одного компонента бинарного раствора равно мольной доле второго компонента в растворе.

Растворы, подчиняющиеся закону Рауля, называются идеальными.

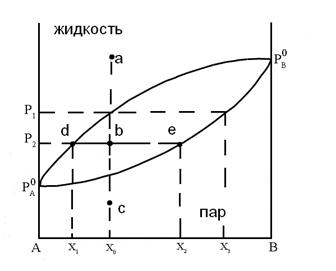
Рис.14 Диаграмма состояния бинарного жидкого

раст­вора и равновесного с ним пара при постоянной температуре.

Любая точка на диаграмме, называемая фигуративной, характеризует сос­тав системы и давления. Выше кри­вой лежит однофазная область - бинарный жидкий раствор, который обладает двумя степенями свободы. Это следует из уравнения (5.8), примененного к точке "а"

Это значит, что для однозначного определения состояния системы с одной фазой нужно задать мольную долю компонента и давление. Бивариантной система будет также в области ниже кривой 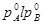, соответствующей однофазной газовой смеси переменного состава.

поле диаграммы, заключенное между кривыми и 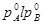, соответствует двухфазной системе: жидкий раствор и равновесный с ним пар. Верхняя кривая характеризует зависимость давления насыщенного пара от состава жидкости и называется линией жидкости (ликвидуса), а кривая 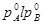– зависимость давления насыщенного пара от состава пара. Это- линия пара. Любая фигуративная точка, заключенная между ветвями жидкости и пара, отвечает системе с одной степенью свободы. Если через точку «b» проведем изобару, то точки ее пересечения с ветвями жидкости (a) и пара (c) будут характеризовать равновесные составы жидкости и пара соответственно. Такие точки, выражающие составы двух равновесных фаз при заданных T и p, называются сопряженными точками, а линии, соединяющие сопряженные точки (dl), называются нодами, или коннодами. Состав пара отличается от состава равновесной с ним жидкости. При изотермическом сжатии ненасыщенного пара состава x₂ фигуративная точка поднимается вверх. В точке «c» пар становится насыщенным, появляются первые капли жидкости состава x₁, то есть жидкость обогащена компонентом А по сравнению с равновесным с ней паром. При изотермическом уменьшении давления точка «а», характеризующая жидкую фазу, смещается вниз и при давлении образуется пар состава x₃ , обогащенный компонентом B по сравнению с жидкой фазой.

Отклонения от закона Рауля.

Для многих систем из двух летучих жидкостей закон Рауля не выполняется. Отклонения давления пара от линейной зависимости в сторону больших значений называют положительными, а в сторону меньших значений – отрицательными. Причина положительных отклонений от закона Рауля заключается в том, что разно­родные молекулы притягиваются слабее однородных. При образова­нии жидкого раствора межмолекулярное взаимодействие ослабляется, и возможность перехода молекул в парообразное состояние увеличивается. При этом давление насыщенного пара будет боль­ше, чем следовало бы по закону Рауля. Отрицательные отклоне­ния от закона Рауля наблюдаются в том случае, когда взаимодействие между разнородными молекулами больше, чем между однород­ными. Это вызывает уменьшение давления насыщенного пара по сравнению с величиной, наблюдаемой для идеальных растворов.

Положительные отклонения от закона Рауля наблюдаются в системах ацетон-этанол, вода-метанол, четыреххлористый угле­род-бензол, четыреххлористый углерод-хлороформ, а отрицатель­ные отклонения от закона Рауля у растворов: вода - азотная кислота, ацетон-хлороформ, бензол-хлороформ.

Законы Вревского.

Первый закон Вревского показывает, как влияет изменение температуры на состав одной из фаз при заданной составе дру­гой фазы: при повышении температуры раствора заданного состава его пар обогащается тем компонентом, парциальная молярная теплота испарения которого больше. Этот закон справедлив как для растворов с азеотропом, так и без него. Азеотропным называется раствор, у которого состав пара совпадает с составом жидкости. На рис. 15 показано влия­ние температуры на состав пара при заданном составе жидкости (без азеотропа). Теплота испарения труднолетучего вещества больше теплоты испарения легколетучего, поэтому равновесный с жидкостью пар с повышением температуры бу­дет обогащаться компонентом А, например, от его мольной доли 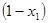до .

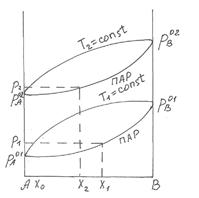
Рис. 15.

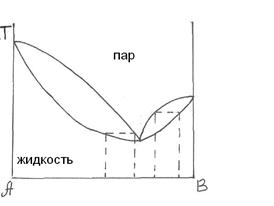Второй закон Вревского относится только к растворам, образующим азеотроп, и указывает направление изменения состава азеотропа с повышением температуры: если на кривой зависимости давления пара от состава раствора имеется максимум, то при повышении температуры в азеотропном растворе возрастает концент­рация того компонента, молярная теплота испарения которого больше. Для систем, имеющих минимум на соответствующих кривых, с повышением температуры в азеотропном растворе возрастает кон­центрация компонента, молярная теплота испарения которого меньше.

Рис. 16.

Понижение температуры замерзания раствора. Криоскопия.

На рис.17 кривая ОС ха­рактеризует давление насыщенного пара над чистым жидким раст­ворителем, а кривая ОА - дав­ление насыщенного пара над твердым растворителем. Точка О характеризует температуру замерзания чистого растворите­ля. 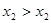После добавления к раство­рителю нелетучего вещества его давление насыщенного пара сог­ласно закону Рауля будет во всем интервале температур по­нижаться, и температурная зависимость давления растворителя будет описываться кривой при концентрации твердого тела , а при концентрации – кривой 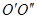. 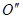Точки и определяют температуру начала за­мерзания растворов с соответствующими концентрациями раство­ренного вещества. Из рис.17 видно, что кристаллизация раство­рителя начинается при тем более низкой температуре, чем выше в нём концентрация растворенного вещества.

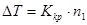, (5.22)

где– понижение температуры замерзания одного килограмма данного растворителя при добавлении к нему одного моля растворенного вещества. называют молярным понижением точки затвердевания раствора, или криоскопической константой, а изучение температур затвердевания растворов называют криоскопией.

По понижению температуры кристаллизации раствора, зная криоскопическую константу, можно определить молекулярную массу растворенного вещества. Определение молекулярной массы растворенного вещества по изучению температуры замерзания растворов называется криоскопическим методом определения молекулярных масс.

(5.22а)

Повышение температуры кипения раствора. Эбуллиоскопия.

Рис. 17.

Предположим, что внешнее давление равно одной атмосфере. Тогда, как видно из рис.17, чистый растворитель закипит при температуре 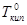. Тогда как пар раствора нелетучего вещества содержит лишь чистый растворитель, то при данной температуре 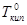давление насыщенного пара раствора 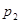(точка М) будет мень­ше давления насыщенного пара чистого растворителя.

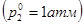Пересечение кривой температурной зависимости давления насыщенного пара над раствором с изобарой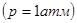произой­дет при температуре (т. N), которая всегда выше темпера­туры кипения чистого растворителя 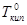(Рис.17). Разность 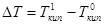будет тем больше, чем больше мольная доля растворенного вещества.

(5.23)

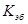– мольное повышение температуры кипения, или повышение температуры кипения идеального раствора, состоящего из одного килограмма растворителя и одного моля растворенного вещества. Величина 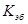называется эбуллиоскопической постоянной, она так же как и криоскопическая постоянная зависит только от природы растворителя.

Уравнение (3.25) дает возможность вычислить молекулярную массу растворенного вещества, измеряя повышение температуры кипения раствора известной весовой концентрации. Метод определе­ния молекулярной массы по уравнению (5.23а) называется эбуллиоскопией.

(5.23а)

Осмотическое давление.

Осмос - это самопроизвольное проникновение растворителя в раствор через полупроницаемую мембрану. Осмотическое давление – это избыточное внешнее давление, которое нужно приложить к раствору, чтобы прекратился поток растворителя через полупроницаемую мембрану, отделяющую его от раствора. Рассмотрим в качестве примера систему, состоящую из двух сосудов (Рис.18), один из которых (1) закрыт внизу мембраной 2, через которую может проходить только растворитель. Сосуд 1 с раствором какого-либо вещества помещен в сосуд­ 3, в котором находится растворитель. Через полупроницаемую мембрану 2 растворитель из сосуда 3 самопроизвольно поступает в сосуд 1, в результате чего там образуется избыточное давление, численно равное осмотическому, но противоположное ему по знаку.

(5.24)

Это выражение носит название уравнение Вант-Гоффа и из него следует, что осмотическое давление разбавленных растворов численно равно давлению, которое производили бы молекулы растворенного в объеме раствора вещества, если бы они в тех же условиях представляли собой идеальный газ.

Дата добавления: 2014-01-06