Бескоалиционные игры

Теория бескоалиционных игр – это способ моделирования и анализа ситуации, в которые оптимальные решения каждого игрока зависит от его представлений (ожиданий) об игреего оппонентов.

Основными предпосылками теории являются следующие.

I. Каждый игрок стремится максимизировать свой выигрыш.

II. Каждый из игроков знает игру.

III. Свои стратегии игроки выбирают одновременно и независимо.

IV. Игра играется однократно.

I. Главная трудность состоит в том, что выигрыш игрока зависит не только от его стратегии, но и от стратегии остальных. Пытаясь уйти от этой неопределенности, теории игр, апеллирует к рациональности. Игрок рационален, если он максимизирует свой ожидаемый выигрыш с учетом всей имеющейся у него информации. Таким образом, первая предпосылка формулируется как предположение рациональности всех игроков.

II. Теория вводит постулат, что знание игры (как и рациональность игроков) является общим знанием: каждый игрок знает не только выигрыши всех игроков, но знает также, что остальные знают, что он знает об этом.

III. Принимая свое решение, игрок не знает о выборе стратегий другими игроками. Отсутствует обмен информации между игроками.

IV. Смысл предпосылки в том, что игроки встретились, сыграли и разошлись, нет ни мести, ни благодарности (трансфертов). Если игра проводится многократно, это уже другая игра.

Каждый игрок должен пытаться предсказать игру своих оппонентов, используя свои знания игры и исходя из предположений, что его оппоненты – сами рациональны, а поэтому пытаются сами также предсказать игру своих оппонентов и максимизировать свои собственные выигрыши.

Платёжная матрица

В общем виде матричная игра может быть записана платёжной матрицей, представленной на рисунке 4.4.

	B1	B2	…	Bn
A1	a11	a12	...	a1n
A2	a21	a22	...	a2n
…	...	...	...	...
Am	am1	am2	...	amn

Рисунок 4.4 - Общий вид платёжной матрицы матричной игры

Здесь A_i – названия стратегий игрока А, B_j – названия стратегий игрока В, a_ij – значения выигрышей игрока 1 при выборе им стратегии i, а игроком 2 – стратегии j. Поскольку данная игра является игрой с нулевой суммой, значение выигрыша для игрока В является величиной, противоположенной по знаку значению выигрыша игрока А.

Пример: Игра поиск. Игрок 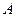прячется в первом или втором месте. Игрок 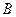ищет его. Если игрок 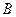находит 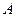, то 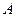платит ему 1 д.е, если же 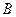не находит 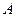, то 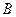платит 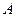1 д.е. Составим платежную матрицу для игры «поиск», рисунок

Рисунок 4.5- Платежная матрица игры «поиск»

Для того, чтобы решить игру, или найти решений игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности: т.е. один из игроков должен получить максимальный выигрыш, когда второй игрок придерживается свое стратегии. В тоже время второй игрок должен иметь минимальный проигрыш, если первый придерживается своей стратегии. Такие стратегии называются оптимальными. Оптимальные стратегии должны удовлетворять условию устойчивости, т.е любому игроку должно быть невыгодно отклоняться от своей стратегии в этой игре.

Каждый из игроков стремится максимизировать свой выигрыш с учётом поведения противодействующего ему игрока. Поэтому для игрока 1 необходимо определить минимальные значения выигрышей в каждой из стратегий, обозначим через 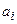эти наименьшие выигрыши при выборе стратегии A_i: 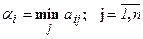. Затем среди всех 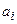выбираем наибольшее: 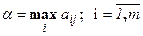. Значение 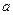называется нижней ценой игр, или максимальным выигрышем (максимином). Это гарантированный выигрыш игрока 1 при любых стратегиях игрока 2: 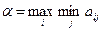. Стратегия, соответствующая максимину, называется максиминной стратегией.

Игрок 2 заинтересован в том, чтобы уменьшить выигрыш игрока А, выбирая стратегию B_j, он учитывает максимально возможный при этом выигрыш для игрока 1, обозначим его через 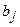: 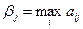. Среди всех чисел 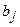выбираем наименьшее и назовем верхней ценой игры или минимаксным выигрышем (минимаксом). Это гарантированный проигрыш игрока 2: 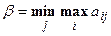. Стратегия, соответствующая минимаксу, называется минимаксной стратегией.

Если верхняя и нижняя цены игры совпадают, то общее значение верхней и нижней цены игры 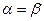называется чистой ценой игры, или ценой игры. Минимаксные стратегии, соответствующие цене игры, являются оптимальными стратегиями, а их совокупность – оптимальным решением, или решением игры. Решение обладает устойчивостью, если один из игроков придерживается своей оптимальной стратегии, то для другого является невыгодным отклоняться от своей оптимальной стратегии. Пара стратегий A_i, и B_j, соответствующий чистой цене игры, называется седловой точкой.

Например, в матрице, показанной на рисунке 4.6 существует решение в чистых стратегиях. При этом для игрока 1 оптимальной чистой стратегией будет стратегия A₁, а для игрока 2 – стратегия B₄. Значения верхней и нижней цен игры равны и достигаются на одной и той же паре стратегий (A₁, B₄). Следовательно игра имеет седловую точку (A₁, B₄) и цена игры равна 4.

	B1	B2	B3	B4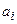
A1
A2
A3

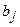
Рисунок 4.6 - Платёжная матрица, в которой существует решение в чистых стратегиях

В матрице на рисунке 4.7 решения в чистых стратегиях не существует, так как нижняя цена игры достигается в стратегии A₁ и её значение равно 2, в то время как верхняя цена игры достигается в стратегии B₄ и её значение равно 3.

	B1	B2	B3	B4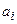
A1
A2
A3

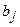
Рисунок 4.7 - Платёжная матрица, в которой не существует решения в чистых стратегиях

Решение игр в смешанных стратегиях

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решений игры (например, игра на рисунке 4.6). В таком случае можно получить оптимальное решений, случайным образом, чередуя чистые стратегии.

Смешанной стратегией S_A игрока А называется применение чистых стратегий А₁, А₂,…,Аm с вероятностями p₁,p₂,…p_m,

Смешанные стратегии обозначаются: 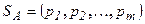для игрока А, 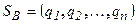- для игрока В, где 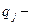вероятность применения стратегии 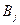. Причем 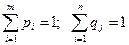– свойство полноты.

С применением смешанных стратегий всегда можно найти решение, обладающее устойчивостью. Решением игры называется пара оптимальных смешанных стратегий 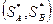обладающих следующим свойством: если один из игроков придерживается своей оптимальной смешанной стратегии, то другому не может быть выгодно отступать от своей. Выигрыш, соответствующий оптимальному решению, называется ценой игры J: .

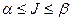Теорема Неймана (основная теорема теории игр). Каждая конечная игра имеет по крайней мере одно решение, возможно в области смешанных стратегий. Цена игры заключена в пределах 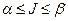. Стратегия, которая входит в оптимальную смешанную стратегию с вероятностью, отличной от нуля, называется активной стратегией.

Теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равен цене игры 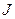независимо от того, если второй игрок не выходит за пределы своих активных стратегий.

Рассмотрим игру 2*2, являющаяся простейшим случаем конечной игры (рисунок 4.8).

Рисунок 4.8 - Платёжная матрица игры 2*2

Если эта игра имеет седловую точку, то оптимальное решение - это пара чистых стратегий, соответствующих этой точке. Если в игре отсутствует седловая точка, то в соответствии с основной теоремой теории игр оптимальное решение существует т определяется парой смешанных стратегий. Чтобы их найти, необходимо воспользовался теоремой об активных стратегиях.

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию, а игрок В – чистую стратегию В₁ - 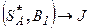(что соответствует первому столбцу матрицы), равен цене игры J и является первым уравнением системы (4.2). Тот же средний выигрыш получит игрок А, если второй игрок применяет стратегию В₂, - 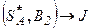, что соответствует второму уравнению системы:

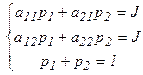. (4.2)

Решая эту систему получим оптимальную стратегию и цену игры:

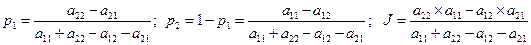, (4.3)

Аналогично применяя терему об активных стратегиях при для отыскания оптимальной стратегии игрока 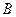, при стратегиях - 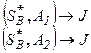имеем:

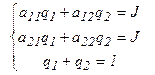, (4.4)

тогда оптимальная стратегия для игрока В определятся формулами:

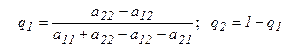. (4.5)

Пример: игра «поиск» задана платежной матрицей (см. рисунок 4.5) без седловой точки. Найдем решение в смешанных стратегиях, применяя полученные выражения (4.3) и (4.5):

, .

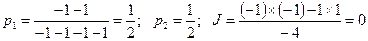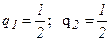Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом, выбирая каждое убежище с вероятностью ½, при этом средний выигрыш составляет 0.

Дата добавления: 2014-01-06