Статистические игры

Теория принятия статистических решений - это чрезвычайно развитая область в экономике, в военном деле, в области обработки информа­ции на фоне шумов и т. д. Рассмотрим элементы этой теории как продолжение теории игр.

Существуют задачи, в которых «бессознательный игрок», который мешает принимать нам принимать правильные решения, но он не противодействует активно, а действует в соответствии с природными случайными явлениями, поэтому такую ситуацию называют игрой с природой, или статистической игрой. С другой стороны, эта «бессознательность» приводит к непредсказуемому поведению противника. Так в теории игр постулируется факт сознательного поведения противника. Поэтому в теории статисти­ческих решений главным является обоснование критериев оценки различных ситуаций со стороны .

Если операция, проводимая системой, уникальна, то для разрешения неопределенности при оценке систем используются субъективные предпочтения ЛПР. По этой причине единого критерия оценки эффективности для неопределенных операций не существует. Разработаны лишь общие требования к критериям и процедурам оценки и выбора оптимальных систем.

В зависимости от характера предпочтения ЛПР наиболее часто в неопределенных операциях используются критерии:

- среднего выигрыша;

- Лапласа;

- Вальда (осторожного наблюдателя);

- максимакса;

- Гурвица (пессимизма-оптимизма);

- Сэвиджа (минимального риска).

Критерий среднего выигрыша. Данный критерий предполагает задание вероятностей состояния природы p_{j .} Эффективность систем оценивается как среднее ожидаемое значение (математическое ожидание) оценок эффективности по всем состояниям природы.

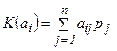, (4.11)

где p_j –вероятность j -го состояния природы.

Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой значение среднего выигрыша максимально:

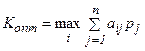. (4.12)

Для применения критерия среднего выигрыша необходим перевод операции из неопределенной в вероятностную, причем произвольным образом.

Критерий Лапласа. Данный критерий используется при наличии неполной информации о вероятностях состояний природы в задаче принятия решения. Вероятности состояний окружающей среды принимаются равными и по каждой стратегии ЛПР в платёжной матрице определяется, таким образом, среднее значение выигрыша:

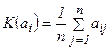. (4.13)

Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой значение среднего выигрыша максимально:

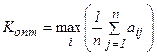. (4.14)

Критерий Лапласа является частным случаем критерия среднего выигрыша.

Критерий Вальда. Это максиминный критерий, который гарантирует определенный выигрыш при наихудших условиях.

Платёжная матрица дополняется столбцом, каждый элемент которого представляет собой минимальное значение выигрыша в соответствующей стратегии ЛПР:

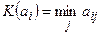. (4.15)

Оптимальной по данному критерию считается та стратегия ЛПР, при выборе которой минимальное значение выигрыша максимально:

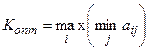. (4.16)

Выбранная таким образом стратегия полностью исключает риск. Это означает, что принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Такая осторожность является в ряде случае недостатком критерия.

Критерий пессимизма-оптимизма Гурвица. Это критерий обобщенного максимина. Стараясь занять наиболее уравновешенную позицию, ЛПР может ввести оценочный коэффициент, называемый коэффициентом пессимизма α, который находится в интервале [0, 1] и отражает ситуацию, промежуточную между точкой зрения крайнего оптимизма и крайнего пессимизма. Данный коэффициент определяется на основе статистических исследований результатов принятия решений или личного опыта принятия решений в схожих ситуациях.

Платёжная матрица дополняется столбцом, коэффициенты которого рассчитываются по формуле:

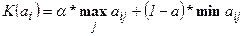. (4.17)

Условие оптимальности записывается в виде:

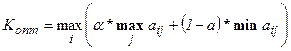. (4.18)

При α =0 критерий Гурвица превращается в критерий максимина. При α = 0 он превращается в критерий максимакса. На практике пользуются хгачениями коэффициента α в пределах 0,3-0,7.

Критерий минимаксного риска Сэвиджа. Минимизирует потери эффективности при наихудших условиях. Платежная матрица должна быть преобразована в матрицу потерь (риска). Каждый элемент матрицы потерь определяется как разность между максимальным и текущим значениями оценок в столбце:

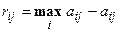. (4.19)

После преобразования матрицы используется критерий минимакса:

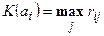, (4.20)

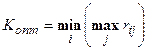. (4.21)

Необходимо отметить, что выбор какого-то критерия приводит к принятию решения по оценке систем, которое может быть совершенно отлично от решений, диктуемых другими критериями

Таким образом, эффективность систем в условиях неопределенности может оцениваться по ряду критериев. На выбор того или иного критерия оказывает влияние ряд факторов:

- природа конкретной операции и ее цель (в одних операциях допустим риск, в других – нужен гарантированный результат);

- причины неопределенности (в одном случае причина неопределенности является случайным результатом действия объективных законов природы, в другом- она вызывается действиями разумного противника, стремящегося помешать в достижении цели);

- характер лица, принимающего решение (одни люди склонны к риску в надежде добиться большего успеха, другие предпочитают действовать всегда осторожно).

Список литературы к главе 4

1. Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении. - М: Финансы и статистика, 2002.

2. Васин А.А., Морозов В.В. Введение в теорию игр с приложениями в экономике. М: 2003.

3. Вентцель Е.С. Исследование операций. – М.: Высшая школа, 2001. –208с.

4. Данилов В.И. Лекции по теории игр. М: РЭШ, 2002.

5. Замков О.О., Черемных Ю.А., Толстопятенко А.В. Математические методы в экономике.– М.: МГУ, Изд-во «Дело и сервис», 1999.

6. Игнатьева А.В., Максимцов М.М. Исследование систем управления. - М.: ЮНИТИ-ДАНА, 2000.

7. Конюховский П. В. Математические методы исследования операций в экономике. - СПб: Питер, 2000.

8. Мулен Э. Теория игр с примерами из математической экономики. М: Мир, 1985

9. Лапшин К.А. Игровые модели принятия решений - методические указания для студентов экономического факультета. - М.: МСХА, 2001.

10. Ларичев О.И. Теория и методы принятия решений. - М.: Логос, 2000.

11. Нейман Д., Моргенштейн О. Теория игр и экономическое поведение. М: Физматгиз, 1970

12. Системный анализ и принятие решений: Словарь-справочник / Под ред. В.Н. Волковой, В.Н. Козлова.- М: Высшая школа, 2004.

13. Chris Shoostarian Business information and decision making. Handbook. Luton business school, 2004

14. J. Cuwin, R. Slaver (2002) Quantitative methods for business decision. Fifth etition

15. D. Waters, Addison –Wesley (1996) Quantitative methods for business

16. Philip Davies Strategy handbook. Luton business school, 2004

Дата добавления: 2014-01-06