Предмет и задачи теории вероятностей

Предмет и задачи теории вероятностей.

Лекция 1

План лекции:

2. Случайные события и их классификация.

Теория вероятностей есть раздел математики, в котором изучаются только случайные явления (события) с устойчивой частотой и выявляются закономерности при массовом их повторении.

Предмет теории вероятности – изучение вероятных закономерностей массовых однородных случайных событий.

Все наблюдаемые при определенных условия события можно разделить на три вида: достоверные, невозможные и случайные. Всякий раз, когда указанные условия выполняются, говорят, что происходит испытание.

Например, стрелок стреляет по мишени, раздельной на 4 области. Выстрел – это испытание. Попадание в определенную область мишени – событие.

Другой пример. В урне имеются цветные шары. Из урны наудачу берут один шар. Извлечение шара из урны есть испытание. Появление шара определенного цвета – событие.

Достоверным называется такое событие, которое происходит при каждом испытании.

Невозможным называется событие, которое не может произойти не при одном испытании.

Случайным называется событие, которое в данном испытании может произойти, а может и не произойти.

Событие «стрелок поразил одним выстрелом сразу 4 области» - невозможное.

Событие «стрелок поразил одну из 4-х областей» - достоверное.

Событие «стрелок поразил 1-ю область» - случайное.

Случайные события обозначаются буквами А,В,С,…, достоверное событие - W (иногда U), невозможное - ø (иногда V)

Суммой события А и В называется такое событие А+В, которое состоится при появлении или события А, или события В, или обоих событий вместе.

Произведением событий А и В называется событие АВ, которое происходит при одновременном наступлении обоих событий.

Аналогично определяется сумма и произведение большего числа событий.

Событие, которое состоится, если событие А произойдет, а событие В не произойдет, называется разностью событий А и В и обозначается А - В.

Если при каждой реализации комплекса условий, когда происходит событие А, происходит и событие В, то говорят, что А влечет за собой В, и обозначают АÌ В или ВÌ А.

Если имеет место одновременно и АÌ В, и ВÌ А, то события А и В называются равносильными (эквивалентными). В этом случае пишут А=В.

События А и В называются несовместными, если их совместное наступление невозможно, т.е. А В = ø

Например, при одном бросании монеты выпадает либо орел (событие А), либо решка (событие В). Событие А и В несовместны.

Два несовместных события А и В называются противоположными, если при всякой реализации комплекса условий одно из них обязательно происходит. Иначе говоря, А и В будут противоположными событиями, если для них одновременно выполняются два соотношения АВ = ø, А + В=W.

Пишут 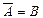Очевидно,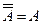

Имеют место важные соотношения (законы де Моргана):

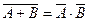
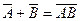
Пример. Событие А – взятая наудачу деталь – 1-го сорта, событие В – 2-го сорта, событие С – 3-го сорта. Что представляют собой следующие

события: А + В;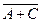; А+С; АС; АВ+С?

Решение. А+В – событие, состоящее в том, что наступит хотя бы одно из событий А и В; следовательно, А+В – деталь 1-го или 2-го сорта. Так как А+С – деталь 1-го или 3-го сорта, то противоположны этому событие 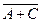– деталь 2-го сорта. АС – невозможное событие, поскольку деталь не может быть одновременно 1-го и 3-го сорта. АВ+С как сумма невозможного события и события с равно С, т.е. АВ+С – деталь 3-го сорта. ■

Пример. Упростить выражение: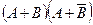

Решение. Используем обычные алгебраические правила раскрытия скобок с учетом действий над событиями:

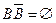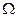Событие АА=А, событие невозможное, поскольку не может одновременно произойти В и противоположное ему, т.е. ; событие , т.е. в скобках имеет достоверное событие (произойдет или В, или не В), таким образом, =А= А.

Теперь запишем окончательное выражение:

(А+В)(А+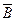)=А+А+ø,=А. ■

Пример. Пусть А,В,С – три произвольных события. Найти выражение для событий, которые состоят в следующем:

1) Произошло одно и только одно событие;

2) Произошло два и только два события;

3) Произошло не более двух событий.

Решение. 1) Данное событие состоит в том, что произошло какое – либо одно из событий А,В или С, и при этом два других события не произошли, т.е. либо событие А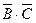, либо событие 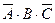, либо событие 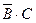. Эти события несовместны, и их можно объединить в сумму:

2). По аналогии с предыдущим: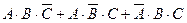

3). Данное событие противоположно событию, состоящему в том, что произошли все три события А, В и С, поскольку все остальные их комбинации подходят под заданное определение. Таким образом, имеем: , или по закону де Моргана: , т.е. хотя бы одно из событий А, В или С не произошло.

События А₁, А ₂,..., А n называются единственно возможными, если в результате испытания приходит какое – либо одно и только одно из этих событий. Говорят также, что эти события образуют полную группу.

Например, игральную кость бросают 1 раз. События А ₁, А ₂, …, А₆ состоят, соответственно в выпадении чисел 1, 2,..., 6. Эти события являются единственно возможными.

Каждое испытание можно описать с помощью событий, которые являются несовместными и единственно возможными. Эти события называются исходами испытания, или элементарными событиями. События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Например, появление герба или решки при бросании монеты – события равновозможные.

Дата добавления: 2014-01-06