Вероятностью события А называется отношение числа исходов, благоприятных событию А, к числу всех исходов испытания

Лекция 2

План лекции:

1. Классическое определение вероятности

2. Относительная частота

3. Геометрические вероятности

Классическое определение вероятности.

Вероятность представляет собой количественную характеристику возможности наступления некоторого случайного события.

Рассмотрим испытания, в результате которого может появиться события А. Каждый исход, при котором осуществляется событие А, называется благоприятным событию А

Например, событие А – «четное число очков при одном бросании игральной кости». Из шести равно возможных исходов (от 1 до 6) три исхода (2, 4, 6) являются благоприятными событию А.

Обозначается вероятность события А через Р (А), т.е.

,

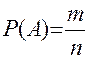где m - число элементарных исходов, благоприятных А, n - число всех исходов.

Здесь предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу. Из определения вероятности вытекают следующие ее свойства:

1) Вероятность достоверного события равна единице:

Р (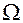) = 1.

2) Вероятность невозможного события равна нулю:

Р (ø) = 0.

3) Вероятность случайного события заключена между нулем и единицей, т.е 0 ≤ P (A) < 1

Недостатки классического определения вероятности:

1.На практике часто встречаются испытания, число возможных исходов которых бесконечно.

2.Очень часто невозможно представить результат испытания в виде совокупности элементарных событий.

3.Далеко не всегда можно считать элементарные события равновозможными.

Построение логически полноценной теории вероятностей основано на аксиоматическом определении случайного события и его вероятности. В системе аксиом, предложенной А.Н. Колмогоровым, неопределяемыми понятиями являются элементарное событие и вероятность.

Рассмотрим аксиомы, определяющие вероятность:

1.Каждому событию А поставлено в соответствие неотрицательное действительное число Р(А). Это число называется вероятностью события А.

2.Вероятность достоверного события равна единице:

Р (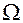) = 1

3.Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий.

Исходя из этих аксиом, свойства вероятностей и зависимости между ними выводят в качестве теорем.

Относительной частотой события А называется отношение числа испытаний, в которых это событие появилось, к общему числу фактически появилось, к общему числу фактически произведенных испытаний, т.е

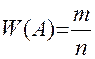
Определение вероятности не требует, чтобы испытания производилось в действительности. Определение относительной частоты предлагает, что испытания были проведены фактически. Вероятность вычислять до опыта, а относительную частоту – после опыта.

Например, если в партии из 80 случайно отобранных деталей ОТК обнаружил 3 нестандартные детали, то относительная частота появления нестандартных деталей равна 3/80.

Если опыты производят в одинаковых условиях, и в каждом из опытов число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало, колеблясь около некоторого постоянного числа. Это постоянное число есть вероятность появления события. Таким образом, относительную частоту можно принять за приближенное значение вероятности.

Пример. Относительные частоты появление герба при бросании монеты в зависимости от числа бросаний отражены в следующей таблице:

Число бросаний	Относительная частота
	0,5069
	0,5016
	0,5005

Дата добавления: 2014-01-06