
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрические вероятности
|
|
|
|
Геометрические вероятности вводят для преодоления неприменимости классического определения вероятности к испытания с бесконечным числом исходов.
Геометрическая вероятность соответствует вероятности попадания точки в области – отрезок, часть плоскости и т.д.
Пусть отрезок ℓ составляет часть отрезка L. На отрезке L наудачу поставлена точка. При этом точка может оказаться в любом месте отрезка L, и вероятность попадания точки на отрезок ℓ пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. Тогда вероятность попадания точки на отрезке ℓ определяется равенством
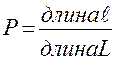
Пример. На отрезке ОА длины L числовой оси ОХ наудачу поставлена точка В (х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую L/3. Вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.
Решение. Разобьем отрезок ОА точками С и Д на 3 равные части. Требование задачи будет выполнено, если точка В(х) попадает на отрезок СД длины L/3. Искомая вероятность
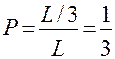

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Это означает, что брошенная точка может оказаться в любом месте G, и вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g. Тогда вероятность попадания точки в фигуру g равна.
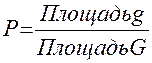
Пример. Задача о встрече. Два студента условились встретиться в определенном месте между 12 и 13 часами дня. Пришедший первым ждет другого ¼ часа, после чего уходит. Найти вероятность того, что встреча состоится, если каждый студент наудачу выбирает время своего прихода между 12 и 13 часами.
Решение. Обозначим время прихода 1-го студента через x,
второго – через y. Встреча должна состояться между 12 и 13 часами, для простоты считаем, что между 0 и 1 часами, т.е.
0 ≤ x ≤ 1, 0 ≤ y ≤ 1
В прямоугольной системе координат это квадрат.
Рассмотрим его как фигуру G.
Встреча состоит, если выполняются неравенства:
y – х ≤ ¼, у > х (1-й студент пришел раньше)
х – у ≤ ¼, х > у (2-й студент пришел раньше)
Этими неравенствами определяется форма фигуры g
 у
у
у > х



 1
1

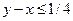
х > у

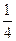
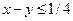 х
х
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 680; Нарушение авторских прав?; Мы поможем в написании вашей работы!