Методы исключения отрезков

В методе перебора, рассмотренном выше, точки , в которых определяются значения 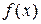, выбираются заранее. Если же для выбора очередной точки вычисления (измерения) 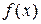использовать информацию, содержащуюся в уже найденных значениях 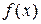, то поиск точки минимума можно сделать более эффективным, т.е. сократить число определяемых для этого значений 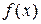), как, например, в методе поразрядного поиска.

Один из путей такого более эффективного поиска точки 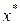указывает свойство 3 унимодальных функций.

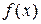Пусть . Сравнив значения в точках и 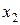(пробных точках), можно сократить отрезок поиска точки 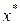, перейдя к отрезку 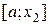, если 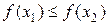, или к отрезку , если (рис. 3.2). Описанную процедуру можно повторить необходимое число раз, последовательно уменьшая отрезок, содержащий точку минимума. Когда длина последнего из найденных отрезков станет достаточно малой, следует положить 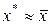, где - одна из точек этого отрезка, например, его середина. Методы минимизации, основанные на этом принципе, называются методами исключения отрезков.

Рис. 3.2. Уменьшение отрезка поиска точки минимума методами исключения отрезков

Чтобы относительное уменьшение отрезка на каждой итерации не зависело от того, какая из его частей исключается из дальнейшего рассмотрения, пробные точки следует располагать симметрично относительно середины исходного отрезка. В зависимости от способа выбора пробных точек получаются различные методы исключения отрезков. На практике используются следующие.

Метод деления отрезка пополам (дихотомии)

Вэтом методе точки и 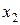располагаются близко к середине очередного отрезка 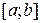, т.е.

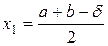, , (3.3)

где - малое число. При этом отношение длин нового и исходного отрезков близко к 1/2, этим и объясняется название метода.

Отметим, что для любых точек и 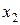величина , поэтому указанный выбор пробных точек объясняется стремлением обеспечить максимально возможное относительное уменьшение отрезка на каждой итерации поиска .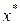

В конце вычислений по методу дихотомии в качестве приближенного значения 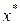берут середину последнего из найденных отрезков 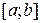, убедившись предварительно, что достигнуто неравенство .

Опишем алгоритм метода деления отрезка пополам.

Шаг 1. Определить и 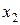по формулам (3.3). Вычислить 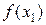и .

Шаг 2. Сравнить 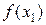и . Если 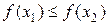, то перейти к отрезку 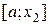, положив , иначе - к отрезку , положив .

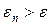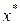Шаг 3. Найти достигнутую точность . Если , то перейти к следующей итерации, вернувшись к шагу 1. Если , то завершить поиск , перейдя к шагу 4.

Шаг 4. Положить , .

Замечание 1. Число из (3.3) выбирается на интервале (0;2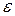) с учетом следующих соображений:

а) чем меньше , тем больше относительное уменьшение длины отрезка на каждой итерации, т.е. при уменьшении достигается более высокая скорость сходимости метода дихотомии;

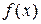б) при чрезмерно малом сравнение значений в точках и 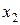отличающихся на величину , становится затруднительным. Поэтому выбор должен быть согласован с точностью определения 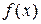и с количеством верных десятичных знаков при задании аргумента х.

Замечание 2. Число 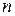итераций метода дихотомии, необходимое для определения точки 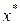с точностью 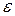, определяется неравенством

(3.4)

В самом деле, обозначим длину исходного отрезка 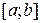через . Длина отрезка, полученного после первой итерации, будет

,

после второй итерации

,

после третьей

и т.д.

Таким образом, в результате 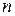итераций длина отрезка поиска точки 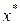станет .

При этом будет достигнута точность определения точки минимума 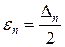. Находя 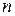из условия

(3.5)

получаем неравенство (3.4)

Замечание 3. Величина может быть выбрана достаточно малой, поэтому, пренебрегая ею в (3.4), получаем: . На каждой итерации метода дихотомии вычисляются два значения 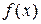. Поэтому после 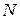вычислений 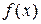производится итераций и достигается точность определения :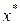

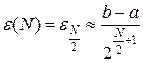(3.6)

Дата добавления: 2014-01-06