Метод золотого сечения

Рассмотрим такое симметричное расположение точек и 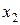на отрезке 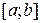, при котором одна из них становится пробной точкой и на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода исключения отрезков, кроме первой, ограничиться определением только одного значения 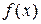, так как другое значение уже найдено на одной из предыдущих итераций.

Найдем точки и 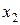, обладающие указанным свойством.

Рассмотрим сначала отрезок и для определенности предположим, что при его уменьшении исключается правая часть этого отрезка. Пусть , тогда симметрично расположенная точка (рис. 3.3).

Рис. 3.3. К определению пробных точек в методе золотого сечения

Пробная точка отрезка перейдет в пробную точку нового отрезка . Чтобы точки и делили отрезки и в одном и том же отношении, должно выполняться равенство или 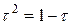, откуда находим положительное значение 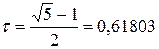…. Таким образом, , .

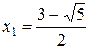Для произвольного отрезка 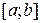выражения для пробных точек примут вид

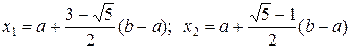(3.7)

Точки и 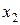из (3.7) обладают следующим свойством: каждая из них делит отрезок 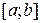на две неравные части так, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньше частей отрезка. Точки с таким свойством называются точками золотого сечения отрезка 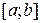. Это и объясняет название рассматриваемого метода.

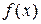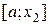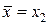На каждой итерации исключения отрезков с пробными точками (3.7) одна из них переходит на следующий отрезок и значение в этой точке вычислять не следует. Если новым отрезком становится , то на него переходит пробная точка исходного отрезка, становясь его второй пробной точкой (рис. 3.3). В случае перехода к отрезку пробная точка исходного отрезка становится первой пробной точкой отрезка .

Легко проверить, что 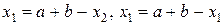. Поэтому на каждой итерации метода золотого сечения недостающую пробную точку нового отрезка можно найти по перешедшей на него пробной точке с помощью сложения и вычитания, не используя формул (3.7).

В конце вычислений по методу золотого сечения в качестве приближенного значения 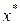можно взять середину последнего из полученных отрезков .

На каждой итерации отрезок поиска точки минимума уменьшается в одном и том же отношении , поэтому в результате 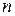итераций его длина становится 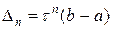. Таким образом, точность , определения точки 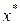после 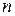итераций находится из равенства

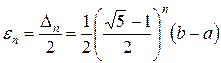, (3.8)

а условием окончания поиска точки 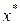с точностью е служит неравенство .

Опишем алгоритм метода золотого сечения.

Шаг 1. Найти и 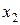по формулам (3.7). Вычислить и . Положить , .

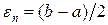Шаг 2. Проверка на окончание поиска: если 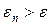, то перейти к шагу 3, иначе — к шагу 4.

Шаг 3. Переход к новому отрезку и новым пробным точкам. Если 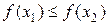, то положить , , , 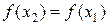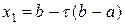и вычислить , иначе - пожить , , 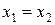, 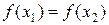и вычислить . Положить 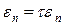и перейти к шагу 2.

Шаг 4. Окончание поиска: положить ,

Замечание. Число итераций, необходимое для достижения заданной точности 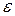, можно найти из условия с учетом соотношения (3.8):

.

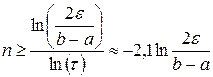Так как 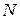вычислений 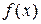позволяют выполнить 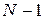итераций метода золотого сечения, то достигнутая в результате этих вычислений точность определения 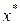составляет

.

Эффективность прямых методов обычно оценивают или по объему вычислений, обеспечивающему заданную точность, или по гарантированной точности, достигнутой в результате выполнения заданного объема вычислений. Поскольку при реализации методов перебора определение значений функции 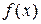требует несравненно больших затрат, чем выполнение таких вспомогательных операций, как вычисление точек перебора, сравнение значений функции и т.п., то объем вычислений можно оценить количеством N вычислений значений функции .

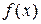Метод считается тем эффективнее, чем меньше 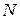, гарантирующее заданную точность определения точки 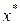минимума функции 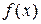. Для сравнения рассматриваемых методов по этому признаку рекомендуется составить таблицу значений в зависимости от требуемой точности определения .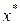

При сравнении методов по точности более эффективным считается тот из рассматриваемых методов, который обеспечивает достижение меньшего значения 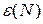при одинаковом объеме вычислений. Для получения вывода о точности рекомендуется составить таблицу значений достигнутой точности 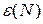в зависимости от количества 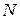найденных значений функции 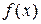для анализируемых методов.

Дата добавления: 2014-01-06