Способы преобразования комплексного чертежа

Общая характеристика способа преобразования комплексного чертежа. Многие задачи решаются легко и просто, если прямые линии, плоские фигуры (основания, грани, ребра, оси) рассматриваемых геометрических тел находятся в частном положении. Такое частное, наивыгоднейшее взаимное расположение геометрического элемента и плоскостей проекций может быть обеспечено преобразованием чертежа.

Трудоемкость и, как следствие, точность графического решения задач часто зависит не только от сложности задачи, но и от того, какое положение занимают геометрические образы, входящие в условие задачи, по отношению к плоскостям проекций.

Для упрощения решения метрических и позиционных задач применяют различные методы преобразования ортогональных проекций. После таких преобразований новые проекции позволяют решать задачу минимальными графическими средствами.

Переход от общего положения геометрического образа к частному можно осуществить изменением взаимного положения проецируемого объекта и плоскости проекции. При ортогональном проецировании это может быть достигнуто двумя путями:

во-первых – перемещением в пространстве проецируемого объекта так, чтобы он занял частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве;

во - вторых – выбором новой плоскости проекций, по отношению к которой проецируемый объект, не меняющий своего положения в пространстве, окажется в частном положении.

Первый способ лежит в основе метода вращения (и как частные случаи: совмещения и плоско-параллельного перемещения); второй – составляет теоретическую базу способа замены плоскостей проекций.

Рассмотрим каждый из этих случаев в отдельности.

Метод перемены плоскостей проекций. Способ замены плоскостей проекций состоит в том, что одна из плоскостей заменяется на новую. Эта плоскость выбирается перпендикулярно оставшейся плоскости проекций. Геометрический элемент при этом не меняет своего положения в пространстве. Новую плоскость располагают так, чтобы по отношению к ней геометрический элемент занимала частное положение, удобное для решения задачи.

Рис. 1.75 Рис. 1.76

Перемену плоскостей проекций можно производить несколько раз.

На рисунке 76 показано преобразование проекции точки А из системы HV в систему HV₁ , в которой вместо фронтальной плоскости проекций введена новая вертикальная плоскость V₁, а горизонтальная плоскость проекций осталась неизменной. Получаем новую систему двух взаимно перпендикулярных плоскостей H и V₁. В новой системе горизонтальная проекция точки осталась неизменной. Проекция a₁^/ точки А на новую плоскость V₁ находится от плоскости H на том же расстоянии что и проекция a ^/ точки А на плоскости V. Это условие позволяет легко строить проекции точки на комплексном чертеже (рис. 77) на новой плоскости проекций.

Используя вышеизложенное сделаем заключение: расстояние от старой проекции точки до старой оси, равно расстоянию от новой проекции точки до новой оси.

Рис. 1.77

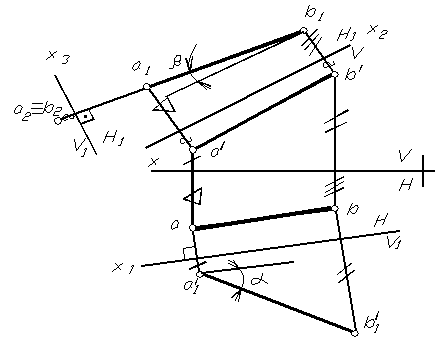
На рисунке 1.77 показано нахождение натуральной величины отрезка АВ и углов наклона его к горизонтальной и фронтальной плоскостям проекций.

При замене фронтальной плоскости проекций V на новую V₁ (она вводится перпендикулярной оставшейся горизонтальной плоскости проекций H и параллельно отрезку АВ) новая ось x₁ проводится параллельно горизонтальной проекции отрезка (x₁ // ab). Используя правило ортогонального проецирования (проекционные линии связи всегда перпендикулярны оси проекций) и условие получения новой проекции точки при замене плоскостей проекций, находим новую проекцию прямой АВ – a₁ ^/ b₁^/

Полученная проекция по величине есть натуральная величина отрезка АВ, здесь же находится угол наклона отрезка к горизонтальной плоскости проекций.

При замене горизонтальной плоскости проекций (новая плоскость вводится параллельной отрезку в пространстве и перпендикулярно оставшейся фронтальной плоскости проекций), получаем опять-таки натуральную величину отрезка и угол наклона его к фронтальной плоскости проекций.

При замене последовательно горизонтальной и фронтальной плоскостей проекции получаем в новой системе плоскостей прямую АВ в виде точки, т. е. в новой системе а прямая становится проецирующей.

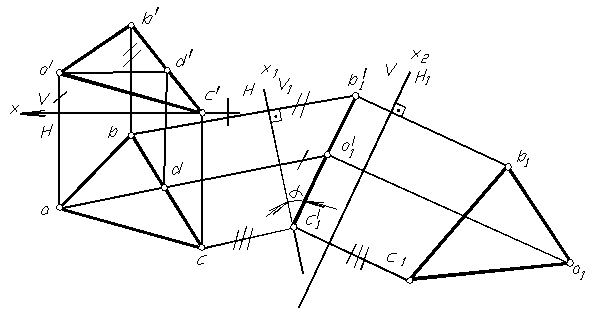
Рис. 1.78

На рисунке 1.78 показано нахождение натуральной величины плоской фигуры – треугольника АВС и угол наклона его к горизонтальной плоскости проекций. Для этого фронтальная плоскость проекций заменена на новую (перпендикулярную оставшейся горизонтальной плоскости проекций и треугольнику АВС) - V₁ . Из условия перпендикулярности прямой и плоскости в треугольнике проведена горизонталь и новая ось x₁ проведена перпендикулярно горизонтальной проекции горизонтали ad. Тогда на новую плоскость V₁ треугольник проецируется в линию и здесь же можно увидеть угол наклона треугольника к горизонтальной плоскости проекций. Далее заменив горизонтальную плоскость проекций на новую, перпендикулярную плоскости V₁ и параллельную плоскости треугольника, получим в новой системе плоскостей натуральную величину треугольника АВС.

Способ вращения. При применении способа вращения плоскости проекций остаются неизменными, а изменяется положение объекта в пространстве. Изменение положения объекта достигается вращением его вокруг некоторой оси. В качестве оси вращения обычно выбирают проецирующую прямую или прямую уровня, т.к. построение, выполняемые на комплексном чертеже при вращении вокруг этих прямых, значительно проще построений при вращении вокруг прямой общего положения.

При вращении вокруг какой-либо оси следует помнить, что вращающаяся точка описывает окружность, расположенную в плоскости, перпендикулярной оси вращения. Центр этой окружности является основанием перпендикуляра, опущенного из вращаемой точки на ось вращения, или, иначе, точкой пересечения с осью вращения плоскости, в которой вращается точка. Совершенно очевидно, что все точки объекта поворачиваются на один и тот же угол.

Т.о. При вращении точки вокруг горизонтальной (фронтальной) проецирующей прямой горизонтальная (фронтальная) проекция точки перемещается по окружности, а фронтальная (горизонтальная) проекция – прямой параллельной оси.

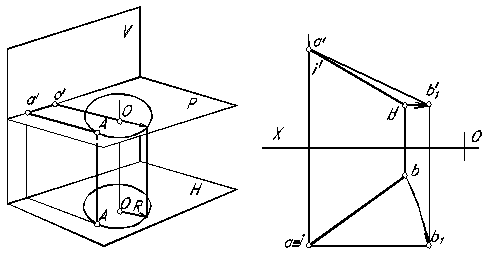
Рис. 1.79

Рассмотрим поворот отрезка прямой линии вокруг заданной оси. При этом, если ось вращения выбрать проходящей через один из концов отрезка, то построение упростится, так как точка, через которую проходит ось, будет неподвижной и для поворота отрезка надо построить новое положение проекций только одной точки – другого конца.

На рисунке 1.79 показан случай, когда для поворота отрезка АВ выбрана ось вращения, перпендикулярная к горизонтальной плоскости проекций, и проходящая через точку А. При повороте вокруг такой оси можно, например, расположить отрезок параллельно фронтальной плоскости проекций. Горизонтальная проекция отрезка в своем новом положении

параллельна оси ОХ. Найдя точку b'₂ и построив отрезок a' b'₂, получаем фронтальную проекцию отрезка АВ в его новом положении. Проекция a' b'₂ выражает длину отрезка АВ. Угол a' b'₂ b' равен углу между прямой АВ и горизонтальной плоскостью проекций.

1.17 Многогранники

Гранной поверхностью называется поверхность, образованная перемещением прямолинейной образующей по ломаной направляющей. Гранные поверхности можно подразделить на два вида: пирамидальные и призматические.

Часть пространства, ограниченная со всех сторон поверхностью, называется телом.

Многогранником называется тело, ограниченное плоскими многоугольниками. Рассмотрение многогранников ограничим рассмотрением призм и пирамид.

Призмой называется многогранник, у которого одинаковые взаимно параллельные грани – основания, а остальные – боковые грани – параллелограммы. Если ребра боковых граней перпендикулярны основанию, то призму называют прямой. Для задания призмы достаточно задать одно ее основание и боковое ребро.

Пирамида представляет собой многогранник, у которого одна грань – произвольный многоугольник, принимающейся за основание, а остальные грани (боковые) – треугольники с общей вершиной, называемой вершиной пирамиды.

Дата добавления: 2014-01-06