Задачи из базы ЕГЭ. Задание B10 (№ 322405) В кармане у Саши было четыре конфеты — «Маска», «Василёк», «Взлётная» и «Коровка»

Задание B10 (№ 322405) В кармане у Саши было четыре конфеты — «Маска», «Василёк», «Взлётная» и «Коровка», а так же ключи от квартиры. Вынимая ключи, Саша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Василёк».

Прототип задания B10 (№ 320200) На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.

Задание B10 (№ 321393) На олимпиаде по химии участников рассаживают по трём аудиториям. В первых двух по 140 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.

Прототип задания B10 (№ 320193) В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрные с жёлтыми надписями на бортах, остальные — жёлтые с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.

Задание B10 (№ 321503) В группе туристов 24 человека. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 3 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист З. полетит первым рейсом вертолёта.

Задание B10 (№ 321297) На борту самолёта 23 мест рядом с запасными выходами и 25 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир З. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру З. достанется удобное место, если всего в самолёте 100 мест.

Задание B10 (№ 321007) В группе туристов 8 человек. С помощью жребия они выбирают четырёх человек, которые должны идти в село за продуктами. Турист Г. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что Г. пойдёт в магазин?

Задание B10 (№ 321053) В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что наступит исход ОРР (в первый раз выпадает орёл, во второй и третий — решка).

Задание B10 (№ 315949) В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что решка выпадет ровно один раз.

Задание B10 (№ 283459) В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.

Задание B10 (№ 320851) На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет больше 2, но меньше 7?

Задание B10 (№ 320375) В чемпионате мира участвуют 12 команд. С помощью жребия их нужно разделить на четыре группы по три команды в каждой. В ящике вперемешку лежат карточки с номерами групп:

1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4.

Капитаны команд тянут по одной карточке. Какова вероятность того, что команда Канады окажется в третьей группе?

Задание B10 (№ 286373) В сборнике билетов по физике всего 20 билетов, в 8 из них встречается вопрос по оптике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по оптике.

Задание B10 (№ 286473) На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 7 прыгунов из Голландии и 2 прыгуна из Боливии. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первым будет выступать прыгун из Боливии.

Задание B10 (№ 320335) Марина, Катя, Вова, Лена, Миша, Артур, Ваня и Сеня бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Ваня.

Задание B10 (№ 286025) Научная конференция проводится в 3 дня. Всего запланировано 50 докладов — в первый день 16 докладов, остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?

Задание B10 (№ 286113) Конкурс исполнителей проводится в 5 дней. Всего заявлено 75 выступлений — по одному от каждой страны. В первый день 27 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?

Задание B10 (№ 286199) На семинар приехали 6 ученых из Великобритании, 7 из Хорватии и 2 из Норвегии. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что первым окажется доклад ученого из Великобритании.

Задание B10 (№ 286303) В сборнике билетов по химии всего 15 билетов, в 6 из них встречается вопрос по солям. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по солям.

Задание B10 (№ 283571) В чемпионате по гимнастике участвуют 40 спортсменок: 12 из Великобритании, 16 из Франции, остальные — из Германии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Германии.

Задание B10 (№ 283619) В среднем из 500 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

Задание B10 (№ 283717) Фабрика выпускает сумки. В среднем на 180 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Задание B10 (№ 283819) В соревнованиях по толканию ядра участвуют 7 спортсменов из Греции, 8 спортсменов из Болгарии, 7 спортсменов из Румынии и 10 — из Венгрии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Болгарии.

Определение. Вероятностным пространством называ­ется любое конечное множество U={U₁, U₂, U₃, ..., U_n}, каждо­му элементу U_k, которого поставлено в соответствие неотрица­тельное число Р_k, 0£P_k£1, называемое его вероятностью. При этом сумма чисел Р_k, k = 1, 2, ..., n, равна единице: P₁+P₂+P₃+…+P_n=1.

Элементы U₁, U₂, U₃, ..., U_n множества U называются исходами, а множество U — множеством исходов.

Замечание. Из определения следует, что исходы U₁, U₂, U₃, ..., U_n множества U попарно не пересекаются, то есть появление одного из них исключает появление других, и в результате опыта один из этих исходов обязательно произойдёт.

После того как мы описали вероятностное пространство, пе­рейдем к описанию событий. В связи с этим введем следующее определение:

Определение. Событием А в данном опыте называется любое подмножество Х множества исходов U. Вероятностью со­бытия А назовем сумму вероятностей исходов, принадлежащих множеству X. Каждый исход, входящий в подмножество X, назы­вается исходом, благоприятствующим событию A.

Если событие A таково, что подмножество Х совпадает с мно­жеством исходов U, то есть

Х = U, то P(A)=P(U₁)+P(U₂)+...+P(U_n)=1 и событие A называют достоверным; если же Х — пустое множе­ство, т. е. Х=Æ, то Р(A)=0 и событие A называют не­возможным.

Рассмотрим пример. Изучим распределение мальчиков и девочек в семьях, имеющих трех детей.

Будем считать, что все дети имеют разный возраст (нет близ­нецов) и что вероятность рождения мальчиков и девочек одинакова и равна 1/2.

Рассмотрим опыт: выбрана семья, имеющая трех разновозра­стных детей. Построим вероятностное пространство этого опыта. Будем буквой М обозначать мальчика, а буквой Д — девочку.

Совпадение вероятностей Р(М)=Р(Д)=1/2 обеспечивает равно­вероятность всех исходов нашего опыта.

Дерево исходов этого опыта имеет вид, изображенный на ри­сунке.

Третий ребёнок

Второй ребёнок

Мальчик (МММ)=U₁

Первый ребёнок Мальчик

Девочка (ММД)=U₂

Мальчик Мальчик (МДМ)=U₃

Девочка

Девочка (МДД)=U₄

Мальчик (ДММ)=U₅

Мальчик

Девочка (ДМД)=U6

Девочка Мальчик (ДДМ)=U₇

Девочка

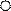Девочка (ДДД)=U₈

Множество всех равновероятных исходов нашего опыта U={U₁, U_2, U₃, U₄, U₅, U₆, U₇, U₈}.

Вероятность каждого исхода равна 1/8. Запишем исходы и их вероятности:

Исходы	U1	U2	U3	U4	U5	U6	U7	U8
Вероятности	1/8	1/8	1/8	1/8	l/8	1/8	1/8	1/8

Сумма вероятностей исходов P(U₁)+P(U₂)+P(U₃)+P(U₄)+P(U₅)+P(U₆)+P(U₇)+P(U₈)=(1/8)·8=1, и поэтому эта таблица задает вероятностное пространство нашего опыта. Рассмотрим некоторое событие А, связанное с рассматриваемым опытом. Пусть, например, событие А — «в семье есть дети обоих по­лов». Событие А совпадает с подмножеством {U_2, U₃, U₄, U₅, U₆, U₇}, множества исходов, и поэтому

P(A)=P(U₂)+P(U₃)+P(U₄)+P(U₅)+P(U₆)+P(U₇)=(1/8)·6=3/4.

Другое событие, связанное с этим опытом, событие В — «в семье есть по крайней мере одна девочка». Это событие совпадает с подмножеством {U_2, U₃, U₄, U₅, U₆, U₇, U₈}, и его вероятность

P(B)=P(U₂)+P(U₃)+P(U₄)+P(U₅)+P(U₆)+P(U₇)+P(U₈)=(1/8)·7=7/8.

Обратим внимание на то, что с изучаемым опытом обычно связа­но несколько вероятностных пространств.

Рассмотрим другие исходы нашего опыта, отличные от исходов полу­ченных выше.

Пусть исход V₁ — «в семье три мальчика», V₂ — «в семье два мальчика и одна девочка», V₃— «в семье один мальчик и две де­вочки» и исход V₄ — «в семье три девочки». Исходы V₁, V₂, V₃ и V₄ взаимно исключают друг друга, и в результате опыта один из них обязательно произойдет. Однако эти исходы равноверо­ятными уже не являются. Действительно, анализируя дере­во исходов, изображенное на рисунке, убеждаемся, что исход V₁ совпадает с исходом U₁ и поэтому Р(V₁)=1/8; исход V₄ совпадает с исходом U₈ и поэтому P(V₄) = 1/8. Исход V₂ наступает тогда, когда наступают исходы U₂, U₃, U₅, и поэтому P(V₂)=3/8. Анало­гично Р(V₃)=3/8. Теперь имеем:

Исходы	V1	V2	V3	V4
Вероятности	1/8	3/8	3/8	1/8

Т а б л и ц а 2

Поскольку сумма вероятностей равна единице:

P(V₁)+P(V₂)+P(V₃)+P(V₄)=1, то таблица 2 задает другое вероятностное пространство нашего опыта и исходы V₁, V₁, V₃ и V₄ образуют множество его исходов

V={V₁, V₁, V₃, V₄}.

В построенном пространстве рассмотрим событие А — «в семье не более одного мальчика». Это событие совпадет с под­множеством {V₃, V₄}, и поэтому

Р(A)=Р(V₃)+Р(V₄)=(3/8)+(1/8)=1/2.

Вопрос о том, какое из вероятностных пространств рассматри­вать, требует тщательного анализа, как условий задачи, так и условий опыта.

В заключение вернемся к вероятностному пространству, за­данному таблицей 2.

Практический смысл этой таблицы состоит в том, что в боль­шой группе, содержащей N трехдетных семей, примерно (1/4) N семей будет иметь детей одного пола, а (3/4) N семей — детей разного пола. Это должны учитывать, например, архитекторы, планируя пропорции между квартирами, имеющими 2, 3, 4 и так далее комнат.

Рассмотрим задания из базы ЕГЭ.

Дата добавления: 2014-01-06