Задачи из базы ЕГЭ

Ответ. 0,125.

Задание B10 (№ 321995) В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,6. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).

Задание B10 (№ 321033) Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Изумруд» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Изумруд» выиграет жребий ровно два раза.

Прототип задания B10 (№ 320186) На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.

13. Задание B10 (№ 321985) Чтобы поступить в институт на специальность «Международное право», абитуриент должен набрать на ЕГЭ не менее 73 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Социология», нужно набрать не менее 73 баллов по каждому из трёх предметов — математика, русский язык и обществознание.

Вероятность того, что абитуриент Л. получит не менее 73 баллов по математике, равна 0,5, по русскому языку — 0,9, по иностранному языку — 0,9 и по обществознанию — 0,7.

Найдите вероятность того, что Л. сможет поступить на одну из двух упомянутых специальностей.

Решение. Не так уж нескоро каждому из вас предстоит сдача ЕГЭ по выбранным вами предметам, с целью продолжения получения образования. Уверен, что многие из вас, для подстраховки, помимо основного направления получения образования рассмотрели и запасные варианты. Возможно, именно поэтому некоторые из вас помимо экзаменов по двум обязательным предметам сдают экзамены по предметам, которые являются конкурсными для поступления на ту или иную специальность. Прежде чем непосредственно перейти к решению задачи, ответим на несколько организационных вопросов, которые к математике не имеют ни какого отношения. «Сколько раз каждый из вас имеет право сдавать ЕГЭ по отдельно взятому предмету?» Вы абсолютно правы, только один раз – один подход. На это мне хотелось бы обратить особое внимание: ровно один раз! «Имеет ли значение, для поступления в ВУЗ порядок расположения предметов в расписании ЕГЭ?» Конечно же, нет!!! «Что, на ваш взгляд, действительно имеет значение для поступления на выбранную вами специальность?» Правильно – результаты ЕГЭ по выбранным вами предметам.

А теперь перейдём к решению задачи. Опыт состоит в сдаче ЕГЭ по четырём предметам. Поскольку порядок сдачи ЕГЭ, по выбранным вами предметам, не имеет значения, то для сохранения интриги будем считать, что последним в расписании ЕГЭ, из четырех упомянутых в условии задачи предметов, стоит математика. Как известно, по результатам ЕГЭ каждому из вас выдаётся свидетельство с указанием тестовых баллов по каждому из четырёх предметов. Давайте подумаем, чем могут отличаться свидетельства учащихся, сдавших те же четыре предмета? Правильно – количеством баллов по каждому из четырех предметов. Как вы думаете, сколько существует различных свидетельств? Действительно, очень много? А что если, с учетом условий задачи, различать свидетельства лишь в зависимости от того каким в сравнении с числом 73 (менее 73 или не менее 73) будет набранный балл по каждому из четырёх предметов. Сколько в этом случае будет различных свидетельств? Согласен, значительно меньше. И все такие свидетельства о результатах ЕГЭ по четырем предметам – русский язык, математика, иностранный язык и обществознание, мы можем рассматривать, как возможные исходы рассматриваемого опыта. А нельзя ли указать все такие исходы? Давайте попробуем!!!

Итак,

предмет	русский язык	иностранный язык	обществознание	математика	ИСХОД
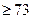
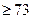
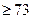
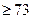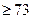
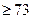
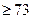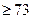
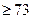
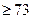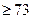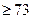
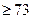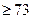
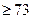
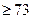
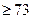
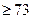
Свидетельство 1 Свидетельство 2 Свидетельство 3 Свидетельство 4 Свидетельство 5 Свидетельство 6 Свидетельство 7	<73 <73 <73	<73 <73 <73	<73 <73 <73	<73	(Р+,И+,О+,М+) (Р+, И+, О+, М-) (Р+, И+, О-, М-) (Р+, И-, О-, М-) (Р-, И-, О+, М+) (Р-, И-, О-, М+) (Р-, И+, О+, М+)
и так далее	и это всего лишь часть свидетельств

Проделанная работа, даёт возможность убедиться в том, что таких исходов будет немало. Возникшая рутинная работа, заставляет задуматься: все ли исходы нам интересны для ответа на главный вопрос задачи? Очевидно, что не все. Нас интересуют лишь те свидетельства, в которых напротив каждого из двух предметов - математика и русский язык, стоит не менее 73 баллов и напротив ровно одного из двух предметов - иностранный язык и обществознание, стоит не менее 73 балов. Таким образом, интересующими нас исходами являются: U={Р+; И+; О-; М+) и W={Р+; И-; О+; М+}, причем, согласно теореме о вероятности совместного осуществления событий независимых в совокупност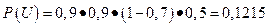и, и 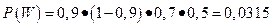. И, наконец, интересующая нас вероятность P равна сумме вероятностей исходов U и W, то есть P=P(U)+P(W)=0,1215+0,0315=0,153.

Ответ. 0,153

Рассмотренный пример может стать яркой иллюстрацией того, что в рамках одного опыта можно построить ни одно множество возможных исходов этого опыта. Действительно, например, исходами, рассмотренного в задаче № 321985, опыта, могут стать всевозможные свидетельства результатов ЕГЭ по четырём предметам – русский язык, математика, иностранный язык, обществознание. Вопрос лишь в том, насколько такое представление неудобно при заданных условиях.

Замечание. Распространенной ошибкой при решении этой задачи, является неверное понимание механизма сдачи ЕГЭ. Учащиеся почему-то считают, что у них есть две возможности сдачи ЕГЭ по математике и по русскому языку. Именно по этой причине учащиеся сначала находят вероятность успешной сдачи экзамена по трём предметам – русский язык, математика и иностранный язык, необходимых для поступления на специальность «Международное право», без учёта результата сдачи ЕГЭ по обществознанию. Затем учащиеся находят вероятность успешной сдачи экзамена по предметам - русский язык, математика и обществознание, без учёта результата ЕГЭ по иностранному языку. При таком неверном способе решения получается солидная вероятность P поступления на одну из специальностей. Действительно, .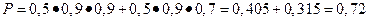

Дата добавления: 2014-01-06