Ответ. 0,32. Прототип задания B10 (№ 320188) Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда

Прототип задания B10 (№ 320188) Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.

Задание B10 (№ 321491) В классе 33 учащихся, среди них два друга — Михаил и Вадим. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Михаил и Вадим окажутся в одной группе.

Решение. Согласно вопросу задачи, нас интересует распределение двух парней по трём группам (для удобства пронумеруем эти группы: группа 1, группа 2 и группа 3). Поэтому возможными исходами рассматриваемого опыта являются:

U₁={Михаил в первой группе, Вадим во второй группе}=(М1, В2),

U₂={Михаил в первой группе, Вадим в третьей группе}=(М1, В3),

U₃={Михаил в первой группе, Вадим в первой группе}=(М1, В1),

U₄={Михаил во второй группе, Вадим в первой группе}=(М2, В1),

U₅={Михаил во второй группе, Вадим во второй группе}=(М2, В2),

U₆={Михаил во второй группе, Вадим в третьей группе}=(М2, В3),

U₇={Михаил в третьей группе, Вадим в первой группе}=(М3, В1),

U₈={Михаил в третьей группе, Вадим во второй группе}=(М3, В2),

U₉={Михаил в третьей группе, Вадим в третьей группе}=(М3, В3),

Таким образом, множество U всех исходов рассматриваемого опыта состоит из девяти элементов U= {U₁, U₂, U₃ ,… U₇, U₉}, причём событию A – «Михаил и Вадим оказались в одной группе» - благоприятствуют лишь три исхода - U₃, U₅ и U₉. Найдём вероятность каждого из этих исходов. Так как по условию задачи класс из 33 человек случайным образом делится на три равных группы, то в каждой такой группе окажется по 11 учащихся этого класса. Исключительно ради удобства решения задачи представим себе 33 стула, расположенных в один ряд, на сидушках которых написаны цифры: на первых 11 стульях написана цифра 1, на следующих 11 стульях – цифра 2 и на последних одиннадцати стульях – цифра 3. Вероятность того, что Михаилу достанется стул с цифрой 1, равна 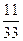(11 стульев с цифрой 1 из общего количества стульев). После того как, Михаил сел на стул с цифрой 1, остаётся лишь 32 стула, среди которых лишь 10 стульев с цифрой 1, поэтому, вероятность того, что Вадиму достанется стул с той же цифрой 1 равна 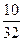. Следовательно, вероятность исхода U₃={Михаил в первой группе, Вадим в первой группе}=(М1, В1) равна произведению 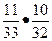и равна 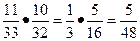. Рассуждая аналогичным образом, находим вероятности исходов U₅ и U₉. Имеем, P(U₅)=P(U₉)=P(U₃)=.

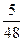Таким образом, P(A)=P(U₃)+P(U₅)+P(U₉)=.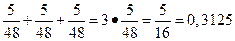

Ответ. 0,3125.

Замечание. Многие учащиеся, составив множество U возможных исходов рассматриваемого опыта, искомую вероятность находят как частное от деления числа исходов U₃, U₅ и U₉, благоприятствующих событию A к числу всевозможных исходов U₁, U₂, U₃ ,… U₇, U₉, то есть P(A)=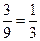. Ошибочность такого решения заключается в том, что исходы рассматриваемого опыта не являются равновероятными. Действительно, P(U₁)=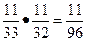, а P(U₃)=.

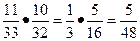Решение. По условию задачи, команда проводит две игры, причем результатом каждой такой игры может быть либо выигрыш, либо проигрыш, либо ничья. А значит, возможными исходами этого опыта являются: U₁={В; В}, здесь и далее В – команда выиграла игру, П – команда проиграла игру, Н – команда сыграла в ничью, U₂={В; Н}, U₃={В; П}, U₄={П; В}, U₅={П; Н}, U₆={П; П}, U₇={Н; Н}, U₈={Н; П}, U₈={Н; В}. Таким образом, множество всевозможных исходов рассматриваемого опыта состоит из 9 элементов, причем событию C – «футбольная команда прошла в следующий круг соревнований» благоприятствуют исходы U₁={В; В}, U₂={В; Н} и U₈={Н; В}, так как наступление каждого из этих исходов гарантирует нужное количество очков для выхода в следующий круг соревнований. Найдем вероятности исходов U₁={В; В}, U₂={В; Н} и U₈={Н; В}. По условию задачи, вероятности выигрыша и проигрыша равны по 0,4, поскольку результатом одной игры может стать либо выигрыш, либо проигрыш, либо ничья, то вероятность ничьи равна разности 1-(U₂+U₈) и равна 0,2. А значит, согласно теореме о вероятности произведения независимых событий, P(U₁)=0,4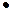0,4=0,16 и P(U₂)=P(U₈)=0,4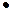0,2=0,08. Итак, искомая вероятность равна: P(C)= P(U₁)+ P(U₂)+P(U₈)=0,16+0,08+0,08=0,32.

Дата добавления: 2014-01-06