Числовые характеристики случайных величин. Функции распределения (интегральная и дифференциальная) являются исчерпывающими характеристиками случайных величин

Лекция 6

Функции распределения (интегральная и дифференциальная) являются исчерпывающими характеристиками случайных величин. Однако часто достаточно найти менее полные, но более простые характеристики, которые отражают самые существенные свойства распределения. Прежде всего нужно знать положение центра, вокруг которого группируются значения СВ и ее разброс относительно этого среднего значения. Среднее значение СВ называется ее математическим ожиданием (МО).

Для дискретной случайной величины, имеющей счетное число значений, задан ряд распределения

Значения случайной величины			…		…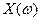
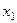
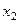
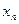
Вероятности			…		…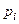

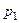
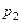
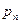
Математическим ожиданием дискретной случайной величины 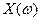называется

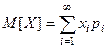.(1)

при условии, что ряд в правой части сходится абсолютно. В этом случае сумма ряда не зависит от порядка расположения слагаемых, т.е. порядок нумерации значений СВ не важен. Если ряд сходится условно или расходится, то соответствующая случайная величина не имеет математического ожидания.

Если дискретная СВ имеет конечное число 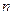значений, то ее математическое ожидание определяется конечной суммой

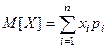(2)

Математическим ожиданием непрерывной случайной величины 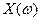называется

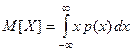(3)

где 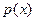– плотность вероятности и несобственный интеграл в правой части (3) сходится абсолютно.

Математическое ожидание это средневзвешенное значение СВ.

Дата добавления: 2014-01-06