Составляющие токов транзистора

Основные допущения идеализированной теории биполярных транзисторов

Расчет токов биполярного транзистора

Для построения идеализированной модели биполярного транзистора будем считать, что его структура разбивается на области пространственного заряда (обедненные области эмиттерного и коллекторного переходов) и квазинейтральные области эмиттера, базы и коллектора, в которых выполняется условие D n» D p. Кроме того, примем обычные допущения идеализированной теории n-p-перехода:

1. Области пространственного заряда практически не содержат подвижных носителей заряда и имеют резкие границы с квазинейтральными областями эмиттера, базы и коллектора.
2. Объемные сопротивления эмиттера, базы и коллектора близки к нулю и внешние напряжения приложены непосредственно к эмиттерному и коллекторному переходам.
3. На краях областей пространственного заряда (на границах переходов) справедливы граничные уравнения, связывающие концентрации носителей заряда с напряжениями, приложенными к переходам.
4. В областях эмиттера, базы и коллектора имеет место низкий уровень инжекции неосновных носителей заряда.

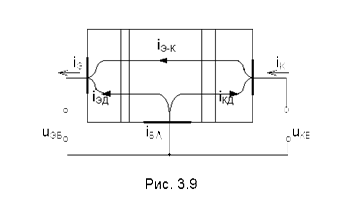
Рассмотрим транзистор, включенный по схеме с ОБ (рис 3.9). Во внешних цепях транзистора будут протекать токи i_Э, i_К, i_Б. За положительные направления токов примем указанные стрелками (они совпадают с физическими направлениями токов в активном режиме). Внешние напряжения u_ЭБ и u_КБ, как и ранее, будем отсчитывать от общего электрода (в данном случае - базы). Кроме того, введем напряжения на переходах транзистора u_ЭП - на эмиттерном переходе, u_{КП -} на коллекторном. Эти напряжения будем считать положительными, если они прямые (“+” приложен к p- области, а “-” к n-области) и отрицательными, если они обратные.

Для рассматриваемого n-p-n-транзистора в схеме с ОБ u_ЭП= - u_ЭБ = u_БЭ и u_КП = - u_КБ. Для p-n-p-транзисторов: u_ЭП= u_ЭБ, u_КП = u_КБ Использование понятий напряжений на переходах позволяет получить одинаковые формулы для n-p-n- и p-n-p-транзисторов.
Как было показано в предыдущей главе, каждый ток содержит различные составляющие; для удобства сгруппируем их следующим образом:

1. Выделим единственную полезную составляющую, обусловленную переносом электронов из эмиттера в коллектор. Назовем ее током связи i_{Э-К к} (направление тока на рис. 3.9 обратно направлению движения электронов).
2. Дырочные токи переходов и токи, обусловленные рекомбинацией в базе, объединим в дополнительные токи эмиттерного i _{э д} и коллекторного i _кд переходов. Эти токи замыкаются каждый через свой переход и не могут передаваться из эмиттера в коллектор. Таким образом, наличие дополнительных токов приводит только к потерям энергии.

Полные токи транзистора могут быть представлены в виде:

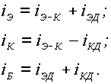(3.1)

Вредные дополнительные токи переходов мало изменяют токи i_Э и i_К (на 1 - 3 %), однако именно они определяют ток базы.

Дата добавления: 2014-01-06