Решение систем линейных алгебраических уравнений

Для решения систем линейных алгебраических уравнений применяют аналитические и численные методы.

Электронная таблица Excel не имеет функций для решения систем уравнений, формулы для вычисления матриц необходимо формировать самостоятельно, используя известные методы, например метод Крамера или метод Гаусса (метод исключения переменных). Однако, используя встроенные функции МОБР, МУМНОЖ и МОПРЕД эти операции выполняются достаточно легко. Например, можно воспользоваться формулой вычисления вектора неизвестных через обратную матрицу и вектор свободнх членов:.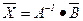

Пример 6.4. Решить систему линейных алгебраических уравнений матричным методом (рис. 6.22):

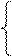2x – 5y + 6z = 8

2x – 4y + 7z = 5 (6.5)

3x – 6y + 8z = -4

Решение.

1. Внесите в ячейки B6 – D8 значения коэффициентов при неизвестных.

2. Внесите в ячейки F6 – F8 значения свободных членов системы уравнений.

3. Выделите диапазон ячеек B12: D14 и введите формулу МОБР(B6:D8), для завершения операции ввода нажмите комбинацию клавиш Ctrl+Shift+Enter.

4. Выделите диапазон ячеек F12:F14 и введите формулу МУМНОЖ(B12:D14;F6:F8). Для завершения ввода формулы нажмите комбинацию клавиш Ctrl+Shift+Enter. В ячейках F12 – F14 появятся значения корней уравнения.

Пример 6.5. Решите систему линейных алгебраических уравнений (6.5) методом Крамера (Листинг 6.9).

Решение.

1. Внесите в таблицу расширенную матрицу, то есть запишите в ячейки A3:D5 электронной таблицы коэффициенты при неизвестных и свободные члены;

2. Запишите в A8:C10 главный определитель, используя в качестве исходных данных адреса ячеек из расширенной матрицы. Этот метод предпочтительнее простого копирования, так как в этом случае при изменении данных в ячейках расширенной матрицы автоматически изменяются и значения в ячейках дополнительного определителя;

3. Cкопировать два раза коэффициенты матрицы из ячеек A8:C10 в ячейки A12:C14 и A16:C18;

Листинг 6.9. Решение системы линейных алгебраических уравнений матричным способом
	A	B	C	D	E	F	G
	Решение системы линейных алгебраических уравнений матричным способом: Х=А^-1B
		Матрица Коэффициентов	Вектор свободных членов
			-5
			-4
			-6			-4
			Обратная матрица		Результат
		-2	-0,8	2,2		-28,8
		-1	0,4	0,4		-7,6
			0,6	-0,4		4,6

4. Cформировать из копий матрицы главного определителя дополнительные определители путем замены коэффициентов при неизвестных на вектор свободных членов. При этом также как и в пункте 2 ссылаться на адреса ячеек D3 – D5;

Листинг 6.10. Решение систем линейных алгебраических уравнений методом Крамера
	А	B	C	D	E	F	G
		Решение систем линейных уравнений методом Крамера
		Главный определитель
			-5		-9
			-4
			-6
		Первый дополнительный		Результат
			-5			X=	-16,00
			-4
		-4	-6
		Второй дополнительный
						Y=	-14,00
			-4
		Третий дополнительный
			-5			Z=	-5,00
			-4
			-6	-4

5. Записать напротив первой строки матрицы коэффициентов главного определителя в ячейку F3 расчетную формулу для его вычисления: МОПРЕД(A3:C5);

6. Скопировать расчетную формулу из ячейки F3 в ячейки F8, скорректировать ее, а затем скопировать в ячейки F12 и F16;

7. Записать формулы для вычисления неизвестных как отношение соответствующих дополнительных определителей к главному определителю в ячейки I3, I4 и I5.

Контрольные вопросы

1. Что такое расширенная матрица коэффициентов системы линейных уравнений?

2. Что является решением системы линейных алгебраических уравнений?

3. Какие методы применяются для решения СЛАУ в электронной таблице?

4. Напишите алгоритм решения САЛУ методом Крамера.

5. Напишите алгоритм решения САЛУ матричным методом с использованием обратной матрицы.

6. Назовите функции электронной таблицы для работы с матрицами.

7. Какие методы используются для решения нелинейных систем уравнений?

Дата добавления: 2014-01-06