КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Вычисление производных численными методами
|
|
|
|
Элементы математического анализа
Если функция задана в виде таблицы, то производные от функции в любой точке могут быть вычислены численными методами по известным приближенным разностным формулам:
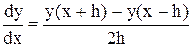O(h) (6.6)
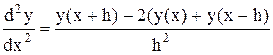O(h2) (6.7)
При вычислении производной численными методами возникают ошибки двух видов: ошибки усечения и ошибки округления.
Ошибка усечения пропорциональна величине шага для первой производной и квадрату величины шага для второй производной. С уменьшением шага ошибка усечения уменьшается, но одновременно возрастает ошибка округления. Чтобы избежать получения ошибочных результатов необходимо контролировать, чтобы разность двух смежных значений функции не была меньше точности вычислений. Например, на компьютере вычисляющем с точностью до 14 знаков, разность не должна быть меньше 10-14 (см. дополнительно раздел 3).
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 410; Нарушение авторских прав?; Мы поможем в написании вашей работы!