Статистика доходностей активов

Для решения поставленного круга задач необходимы знания, хотя бы приближенных параметров для активов и коэффициентов корреляции 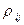для каждой пары активов. Эти параметры могут быть оценены статистическими методами на основе прошлых наблюдений. Ограничимся для простоты случаем двух активов. Пусть к примеру это будут твердые валюты -североамериканский доллар ($) и евро (€). Выбор этих активов объясняется широкой доступностью статистики курсов и ее объективностью. Имея n наблюдений – валютные курсы в

рублях за n последовательность дней

$	х1	х2	…	xn
€	у1	у2	…	уn

рассчитаем дневную доходность вложений, приходящихся на один рубль вложений для каждого актива

$			…
€			…

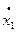
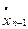
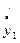
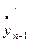
где ,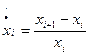

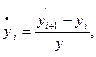
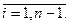
Считая эти значения наблюдениями над случайными величинами и - доходностями за будущий день, можно найти статистические оценки параметров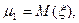

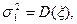
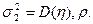
Именно

= =

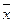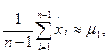
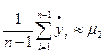
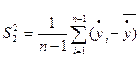²²

Отметим, что число наблюдений не должно быть слишком малым и не должно быть слишком большим. Кроме того, очевидно, что подобная статистика бесполезна в дни паники, когда рыночные цены активов меняются в соответствии с другими законами.

Пример 1. Рассмотрим в качестве активов твердые валюты – североамериканский доллар, и евро. Пусть параметры доходностей за один день принимают значение в масштабе 10^-3 ед.

S₁=0,1; S₂ = 0,1;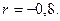

В этом случае средняя доходность портфеля

имеет график

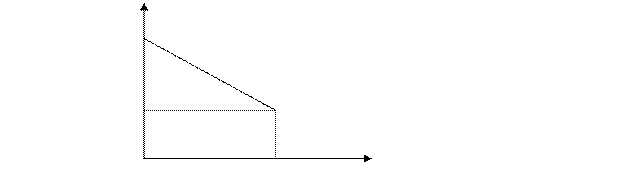
0,5

0,3

0 1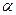

Следовательно, оптимальный по доходности портфель имеет вид (0,1).

Риск портфеля измеряется функцией (3) вида

имеющая график

0,04

0,01

0,005

0 0,68 1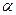

Оптимальным по риску здесь является портфель .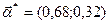

Его доходность

Множество Парето портфелей не мажорирующих друг друга может быть изображено здесь куском параболы на графике

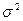
0,04

0,005 0 0,364 0,5

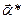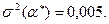Итак, оптимальный по доходности портфель имеет характеристики , а оптимальный по риску портфель соответственно - Уменьшение риска в восемь раз оплачивается уменьшением средней доходности в полтора раза.

Приведенные модели являются лишь стартовым пунктом для построения более сложных моделей инвестирования (см., например, [14]).

Дата добавления: 2014-01-06