Математическое ожидание дискретной случайной величины. Числовые характеристики дискретных случайных величин

Числовые характеристики дискретных случайных величин

Закон распределения полностью характеризует случайную величину. Часто этот закон неизвестен и приходится ограничиться меньшими сведениями. Часто выгоднее пользоваться числами, которые описывают случайную величину в среднем. Такие числа называют числовыми характеристиками случайной величины. К числу важных числовых характеристик относятся: математическое ожидание, дисперсия, среднее квадратическое отклонение. Эти параметры дают о случайной величине значительно меньше сведений, чем закон ее распределения, но для решения многих практических задач они оказываются достаточными.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

Если случайная величина принимает значения 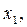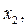…,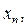вероятности которых соответственно равны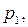 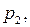…,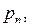то математическое ожидание 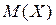случайной величины определяется равенством

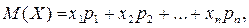
где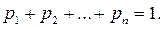

Если дискретная случайная величина принимает счетное множество возможных значений, то

.

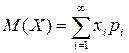Математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.

Пример 1. Найти математическое ожидание случайной величины , зная закон ее распределения:

3 5 2

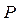0,1 0,6 0,3

Решение. Искомое математическое ожидание равно сумме произведений значений случайной величины на их вероятности

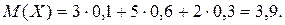
Пример 2. Найти математическое ожидание числа появлений события 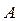в одном испытании, если вероятность события 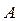равна .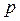

Решение. Случайная величина может принимать только два значения: 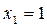- событие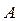наступило с вероятностью 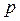и 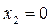- событие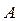не наступило с вероятностью 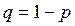. Тогда искомое математическое ожидание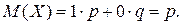

Математическое ожидание числа появлений события в одном испытании равно вероятности этого события.

Дата добавления: 2014-01-06