Неравенство Чебышева. Нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин

Замечания

Нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые невозможно. Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.

Для практики важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая и позволяет предвидеть ход явлений. Эти условия указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли. Для доказательства этих теорем используется неравенство Чебышева.

Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин.

Рассмотрим дискретную случайную величину 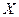, заданную таблицей распределения:

….

….

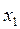
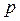
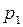
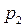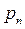
Поставим задачу, оценить вероятность того, что отклонение случайной величины от ее математического ожидания не превышает по абсолютной величине положительного числа 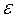. Чебышев П.Л. доказал неравенство, позволяющее дать интересующую нас оценку.

Неравенство Чебышева. Вероятность того, что отклонение случайной величины 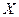от ее математического ожидания по абсолютной величине меньше положительного числа 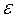, не меньше, чем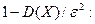

.

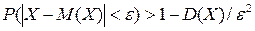Дата добавления: 2014-01-06