
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сводка теории. При использовании формального определения формулы алгебры логики запись формул часто содержит «лишние» скобки
|
|
|
|
При использовании формального определения формулы алгебры логики запись формул часто содержит «лишние» скобки, которыми можно пренебрегать без ущерба для смысла, если применять некоторые общепринятые правила.
Во-первых, в отдельно стоящих формулах (или если границы формулы ясны из контекста) можно опускать внешние скобки.
Во-вторых, как и арифметические операции, связки и кванторы можно упорядочить по их «силе», т.е. расположить в определенном порядке, считая, что те символы, которые в этом порядке находятся правее, «связывают сильнее», т.е. их следует выполнять в первую очередь:
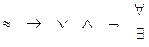
Таким образом, дизъюнкция и конъюнкция связывают сильнее, чем импликация, но слабее, чем отрицание. Конъюнкция связывает сильнее дизъюнкции. Слабее всего связывает эквивалентность. Равноправны в отношении связывания кванторы (об этом подробно в разделе 2), они связывают сильнее, чем любые логические связки.
По сравнению с общим определением формулы формального языка для формул логики высказываний (далее в этом разделе – просто формул) внесем следующие уточнения:
1) в качестве пропозициональных букв (индивидных переменных) будем рассматривать только простые высказывания x, y, z,... 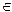 B, B ={ 1, 0 };
B, B ={ 1, 0 };
2) сложные формулы из простых будем строить только с помощью логических операций и скобок.
При таком подходе любая формула будет полностью определяться своей таблицей истинности.
Булевой функцией (или функцией алгебры логики,логической функцией) называется всякая функция n переменных (n = 1, 2,...) с областью определения 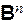 , множество значений которой содержится в B.
, множество значений которой содержится в B.
Любую булеву функцию можно, очевидно, задать таблицей истинности точно такого же вида, как те таблицы, которые сопоставляются формулам. Если таблица истинности, задающая булеву функцию f, совпадает с таблицей истинности некоторой формулы Ф, то говорят, что формула Ф представляет (или задает, или реализует) функцию f.
Две формулы Ф и 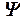 называются равносильными (что обозначается Ф
называются равносильными (что обозначается Ф 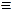
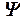 ), если они представляют одну и ту же булеву функцию.
), если они представляют одну и ту же булеву функцию.
Для любых двух формул не представляет никаких трудностей проверить, равносильны ли они: достаточно сравнить их истинностные таблицы.
Булевы функции (от любого числа переменных), принимающие значение 1 независимо от значений аргументов, называются (как и реализующие их формулы) тавтологиями (или тождественно-истинными).
Булевы функции (и реализующие их формулы), всегда принимающие значение 0, называются противоречиями (или тождественно-ложными).
Убедиться в тождественной истинности или тождественной ложности конкретной формулы можно по той же таблице истинности (итоговый столбец таблицы будет содержать только соответствующую константу).
Другой способ доказательства равносильности формул или проверки их тождественной истинности или ложности состоит в использовании так называемых основных логических законов (основных равносильностей), обоснование которых можно провести путем построения соответствующих таблиц истинности. К основным логическим законам обычно относят следующие соотношения:
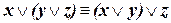
| (ассоциативность дизъюнкции) | (I.1) |
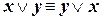
| (коммутативность дизъюнкции) | (I.2) |
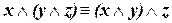
| (ассоциативность конъюнкции) | (I.3) |
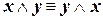
| (коммутативность конъюнкции) | (I.4) |
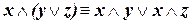
| (дистрибутивность конъюнкции по отношению к дизъюнкции) | (I.5) |
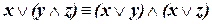
| (дистрибутивность дизъюнкции по отношению к конъюнкции) | (I.6) |
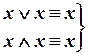
| (идемпотентность или «законы поглощения») | (I.7) (I.8) |
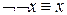
| («закон отрицания отрицания») | (II.1) |
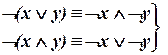
| («законы де Моргана») | (II.2) (II.3) |
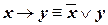
| (III.1) | |
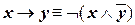
| (III.2) | |
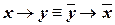
| («закон контрапозиции») | (III.3) |
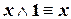
| (IV.1) | |
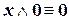
| (IV.2) | |
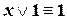
| (IV.3) | |
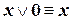
| (IV.4) | |
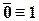
| (IV.5) | |
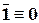
| (IV.6) | |
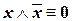
| («закон противоречия») | (IV.7) |
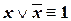
| («закон исключенного третьего») | (IV.8) |
Результаты вычислений таблиц истинности обеих частей равносильностей не зависят от того, как получены значения переменных, входящих в эти соотношения, т.е. от того, являются ли эти переменные независимыми или, в свою очередь, получены в результате каких-либо вычислений. Поэтому приведенные равносильности остаются справедливыми при подстановке вместо переменных любых логических функций и, следовательно, любых формул, представляющих эти функции. Важно лишь соблюдать следующее правило подстановки формулы вместо переменной: при подстановке формулы Ф вместо переменной x все вхождения переменной x в исходное соотношение должны быть одновременно заменены формулой Ф.
Во всякой алгебре (в том числе и в булевой алгебре функций) соотношение
Ф 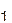
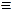 Ф
Ф 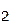 означает, что формулы Ф
означает, что формулы Ф 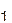 и Ф
и Ф 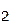 описывают одну и ту же булеву функцию f. Следовательно, если какая-либо формула Ф содержит Ф
описывают одну и ту же булеву функцию f. Следовательно, если какая-либо формула Ф содержит Ф 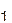 в качестве подформулы, то замена Ф
в качестве подформулы, то замена Ф 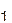 на Ф
на Ф 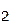 не изменяет элемента булевой алгебры f, над которым производятся операции в формуле Ф; поэтому Ф ', полученная из Ф такой заменой, равносильна Ф. Это утверждение есть правило замены подформул, которое позволяет по имеющимся равносильностям получать формулы, равносильные данной.
не изменяет элемента булевой алгебры f, над которым производятся операции в формуле Ф; поэтому Ф ', полученная из Ф такой заменой, равносильна Ф. Это утверждение есть правило замены подформул, которое позволяет по имеющимся равносильностям получать формулы, равносильные данной.
Отметим разницу между правилами подстановки и замены. При подстановке переменная заменяется на формулу; формула может быть любой, но требуется одновременная ее подстановка вместо всех вхождений переменной. При замене подформул заменяется любая подформула, однако не на любую другую, а только на равносильную ей. При этом замена всех вхождений исходной подформулы не обязательна.
Пусть имеется равносильность Ф 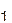
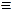 Ф
Ф 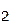 , где Ф
, где Ф 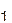 и Ф
и Ф 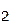 содержат переменную x. Если вместо всех вхождений x в Ф
содержат переменную x. Если вместо всех вхождений x в Ф 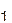 и Ф
и Ф 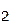 подставить произвольную формулу Ф, то получатся новые формулы Ф '
подставить произвольную формулу Ф, то получатся новые формулы Ф '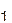 и Ф '
и Ф ' 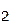 , причем не обязательно Ф
, причем не обязательно Ф 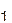
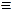 Ф '
Ф '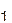 и Ф
и Ф 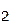
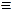 Ф '
Ф ' 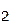 ; однако между собой новые формулы равносильны: Ф '
; однако между собой новые формулы равносильны: Ф '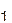
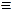 Ф '
Ф ' 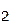 . Если же в Ф
. Если же в Ф 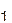 какую-либо подформулу заменить на равносильную ей, то получится новая формула Ф '
какую-либо подформулу заменить на равносильную ей, то получится новая формула Ф '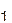 , равносильная Ф
, равносильная Ф 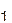 .
.
Такие преобразования, использующие равносильности формул (запас которых можно расширять с помощью правила подстановки) и правило замены, называются тождественными преобразованиями. Тождественные преобразования являются мощным средством доказательства равносильности формул и тождественной истинности или тождественной ложности формул, как правило, более эффективным, чем их вычисление на наборах значений переменных (т.е. чем составление таблиц истинности).
Отметим, что «тактика» доказательства равносильности может быть разная: либо преобразуем одну из формул, приводя ее к виду другой, либо преобразуем обе формулы, приводя их к одной и той же формуле.
|
|
|
Дата добавления: 2014-01-06; Просмотров: 502; Нарушение авторских прав?; Мы поможем в написании вашей работы!