П. 4.2. Аксиомы, тождества и основные законы алгебры логики

И

F7(x) (дизъюнкция или логическое сложение),

которые совместно с функцией инверсии составляют функционально полную систему логических функций.

С помощью этих трех функций (инверсии, конъюнкции и дизъюнкции) можно представить (аналитически выразить) любую сколь угодно сложную логическую функцию.

Очень важной для вычислительной техники является логическая функция исключающее ИЛИ (неравнозначность, сложение по модулю два).

Функция исключающее ИЛИ обозначается символом .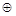

Ниже приведены таблицы истинности для этих четырех функций.

Инверсия

	Конъюнкция	Дизъюнкция	Исключающее ИЛИ

Логические переменные, объединенные знаками логических операций, составляют логические выражения.

При определении значения логического выражения принято следующее старшинство (приоритет) логических операций:

сначала выполняется инверсия,

затем конъюнкция

и в последнюю очередь — дизъюнкция.

Для изменения указанного порядка используют скобки.

В алгебре логики рассматриваются переменные, которые могут принимать только два значения: 0 и 1.

Базируется алгебра логики на отношенииэквивалентности и трех упомянутых ранее операциях:

дизъюнкции (синонимы — логическое сложение, операция ИЛИ),

конъюнкции (логическое умножение, операция И)

и отрицании (инверсия, операция НЕ).

Отношение эквивалентности обозначается знаком =.

Дизъюнкция обозначается знаком 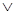, а иногда символом +.

Конъюнкция обозначается символом 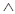, либо точкой , которую можно опускать.

Отрицание обозначается чертой над переменной

Алгебра логики определяется следующей системой аксиом

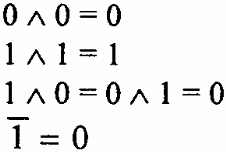
Если в аксиомах произвести взаимную замену операций дизъюнкции и конъюнкции, а также элементов 0 и 1, то из одной аксиомы данной пары получается другая.

Это свойство называется принципом двойственности.

С помощью аксиом можно получить ряд тождеств:

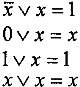
Перечислим законы алгебры логики:

= переместительный (или коммутативный)

= сочетательный ( или ассоциативный)

= распределительный (или дистрибутивный)

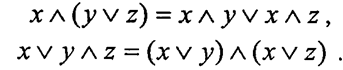
= законы двойственности (или де Моргана)

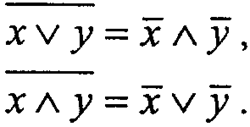
Дата добавления: 2014-01-06